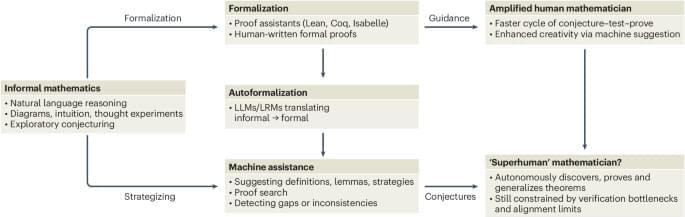
A century ago, the strange behavior of atoms and elementary particles led physicists to formulate a new theory of nature. That theory, quantum mechanics, found immediate success, proving its worth with accurate calculations of hydrogen’s emission and absorption of light. There was, however, a snag. The central equation of quantum mechanics featured the imaginary number i, the square root of −1.
Physicists knew i was a mathematical fiction. Real physical quantities like mass and momentum never yield a negative amount when squared. Yet this unreal number that behaves as i2 = −1 seemed to sit at the heart of the quantum world.
After deriving the i-riddled equation — essentially the law of motion for quantum entities — Erwin Schrödinger expressed the hope that it would be replaced by an entirely real version. (“There is undoubtedly a certain crudeness at the moment” in the equation’s form, he wrote in 1926.) Schrödinger’s distaste notwithstanding, i stuck around, and new generations of physicists took up his equation without much concern.