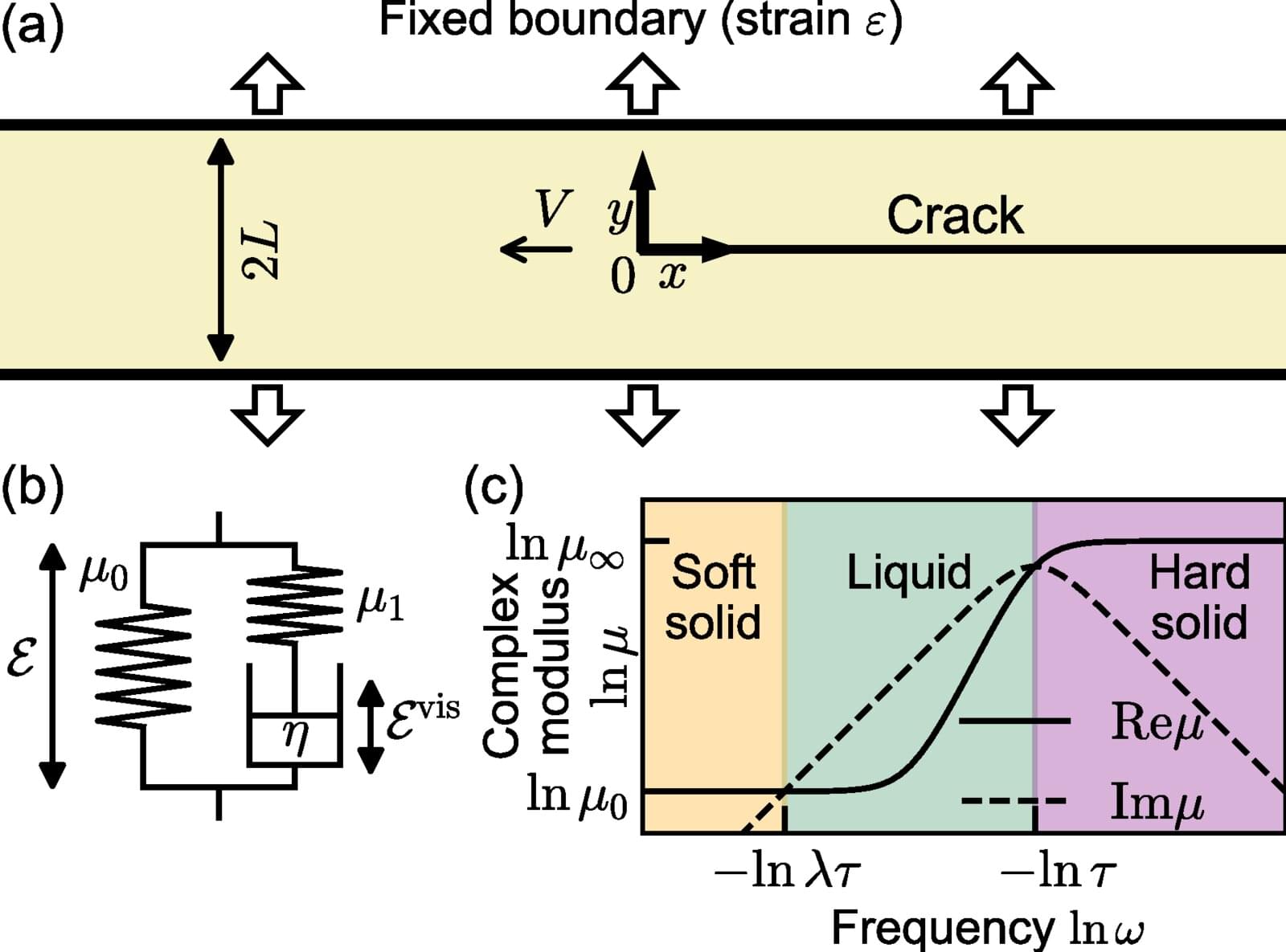
A research group from the University of Osaka, Zen University, and the University of Tokyo has mathematically uncovered the mechanism that causes crack tips to sharpen during the rapid fracture of rubber.
The bursting of rubber balloons or tire blowouts is caused by rapid fracture, a phenomenon in which a small crack propagates instantaneously. During this process, the crack tip sharpens, accelerating the fracture. However, the reason behind this sharpening had long remained unexplained. Traditionally, it was believed to result from the material’s complex nonlinear effects.
The research group—comprising Hokuto Nagatakiya, a doctoral student; Shunsuke Kobayashi, assistant professor; and Ryuichi Tarumi, professor at the University of Osaka; along with Naoyuki Sakumichi, associate professor at Zen University and project associate professor at the University of Tokyo—has mathematically solved the problem of crack propagation. They derived equations that describe both the shape of the crack and the overall deformation of the material.