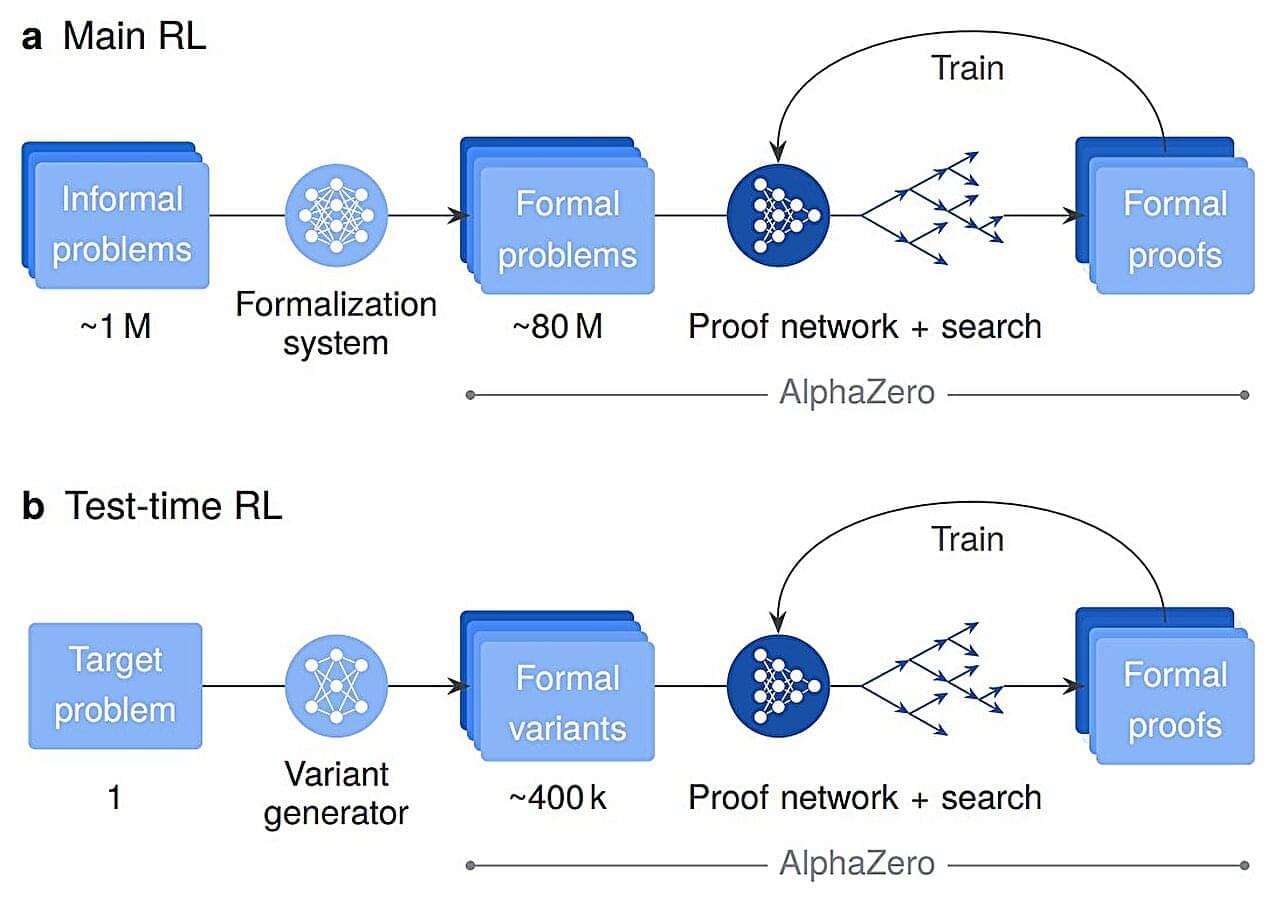
At the 2024 International Mathematical Olympiad (IMO), one competitor did so well that it would have been awarded the Silver Prize, except for one thing: it was an AI system. This was the first time AI had achieved a medal-level performance in the competition’s history. In a paper published in the journal Nature, researchers detail the technology behind this remarkable achievement.
The AI is AlphaProof, a sophisticated program developed by Google DeepMind that learns to solve complex mathematical problems. The achievement at the IMO was impressive enough, but what really makes AlphaProof special is its ability to find and correct errors. While large language models (LLMs) can solve math problems, they often can’t guarantee the accuracy of their solutions. There may be hidden flaws in their reasoning.
AlphaProof is different because its answers are always 100% correct. That’s because it uses a specialized software environment called Lean (originally developed by Microsoft Research) that acts like a strict teacher verifying every logical step. This means the computer itself verifies answers, so its conclusions are trustworthy.