For over a decade, mathematicians have failed to agree whether a 500-page proof is actually correct. Now, translating the proof into a computer-readable form may finally settle the matter



Could a tunnel through space and time—long a dream of science fiction—ever exist in theory? According to Arya Dutta, a Ph.D. student in Mathematics at the Katz School, the answer might be yes, at least on paper.
Accepted for publication in the International Journal of Geometric Methods in Modern Physics, Dutta’s study, “Thin-shell Wormhole with a Background Kalb–Ramond Field,” explored a mathematical model of a wormhole—a hypothetical shortcut through spacetime that could, in theory, connect two distant regions of the universe. “A wormhole allows faster-than-light travel or even time travel,” said Dutta. “It hasn’t been observed yet, but theoretical research has advanced a lot.”

As the C language, which forms the basis of critical global software like operating systems, faces security limitations, KAIST’s research team is pioneering core original technology research for the accurate automatic conversion to Rust to replace it. By proving the mathematical correctness of the conversion, a limitation of existing artificial intelligence (LLM) methods, and solving C language security issues through automatic conversion to Rust, they presented a new direction and vision for future software security research.
The paper by Professor Sukyoung Ryu’s research team from the School of Computing was published in the November issue of Communications of the ACM and was selected as the cover story.
The C language has been widely used in the industry since the 1970s, but its structural limitations have continuously caused severe bugs and security vulnerabilities. Rust, on the other hand, is a secure programming language developed since 2015, used in the development of operating systems and web browsers, and has the characteristic of being able to detect and prevent bugs before program execution.


In mathematical analysis, the Kakutani fixed-point theorem is a fixed-point theorem for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex, compact subset of a Euclidean space to have a fixed point, i.e. a point which is mapped to a set containing it. The Kakutani fixed point theorem is a generalization of the Brouwer fixed point theorem. The Brouwer fixed point theorem is a fundamental result in topology which proves the existence of fixed points for continuous functions defined on compact, convex subsets of Euclidean spaces. Kakutani’s theorem extends this to set-valued functions.
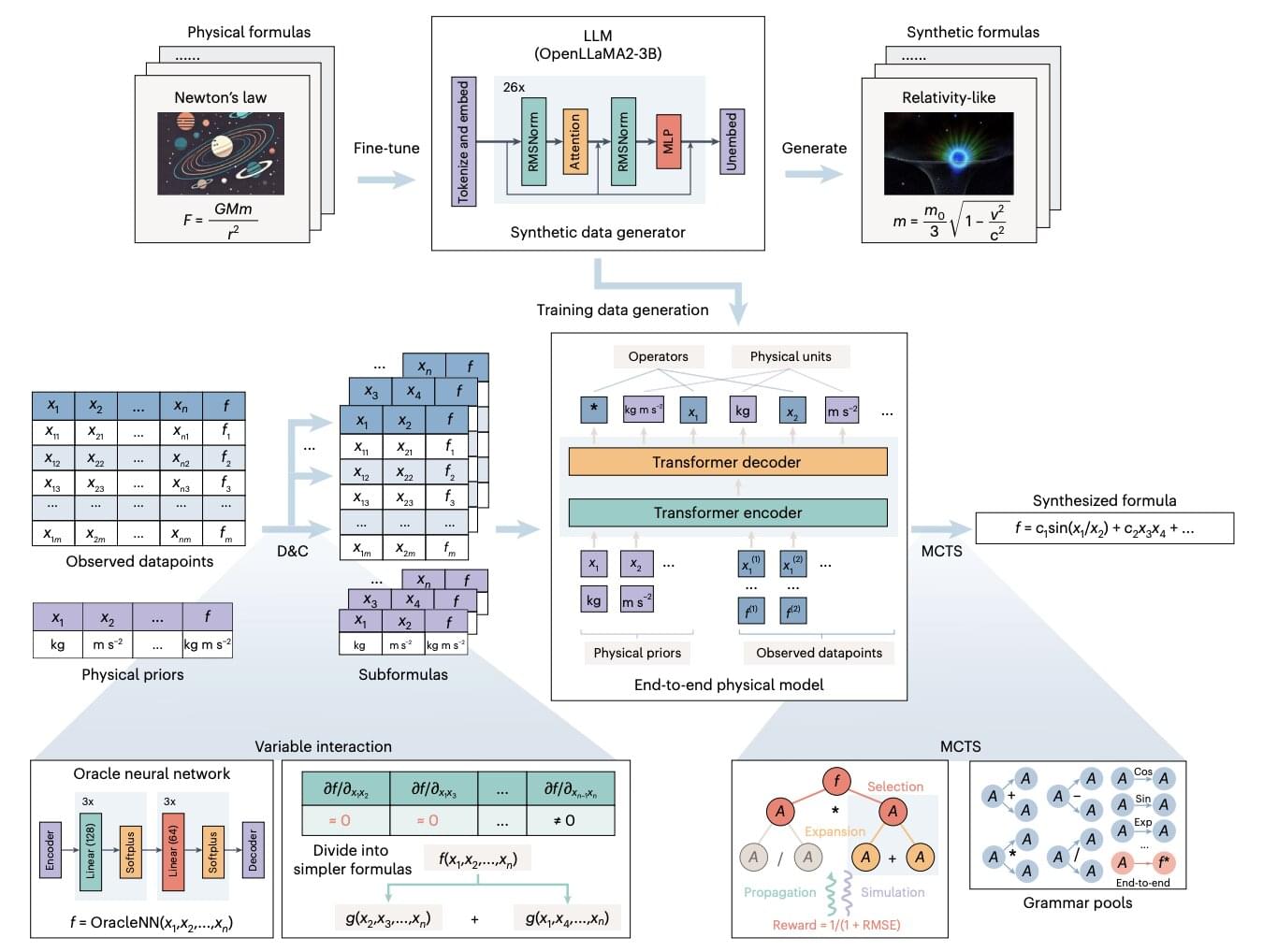
Artificial intelligence (AI) systems, particularly artificial neural networks, have proved to be highly promising tools for uncovering patterns in large amounts of data that would otherwise be difficult to detect. Over the past decade, AI tools have been applied in a wide range of settings and fields.
Among its many possible applications, AI systems could be used to discover physical relationships and symbolic expressions (i.e., mathematical formulas) describing these relationships.
To uncover these formulas, physicists currently need to extensively analyze raw data, thus automating this process could be highly advantageous.

A century ago, the strange behavior of atoms and elementary particles led physicists to formulate a new theory of nature. That theory, quantum mechanics, found immediate success, proving its worth with accurate calculations of hydrogen’s emission and absorption of light. There was, however, a snag. The central equation of quantum mechanics featured the imaginary number i, the square root of −1.
Physicists knew i was a mathematical fiction. Real physical quantities like mass and momentum never yield a negative amount when squared. Yet this unreal number that behaves as i2 = −1 seemed to sit at the heart of the quantum world.
After deriving the i-riddled equation — essentially the law of motion for quantum entities — Erwin Schrödinger expressed the hope that it would be replaced by an entirely real version. (“There is undoubtedly a certain crudeness at the moment” in the equation’s form, he wrote in 1926.) Schrödinger’s distaste notwithstanding, i stuck around, and new generations of physicists took up his equation without much concern.

For obvious reasons, we do not know what the inside of a black hole looks like. But thanks to theoretical physics, we can ask what the inside should look like if Einstein’s theory of gravity and the rules of quantum mechanics are both true. A new study published in the journal Physical Review Letters has done exactly this by concentrating on two black holes that are deeply entangled (linked together by quantum rules).
The research by scientists from the U.S. and Argentina theoretically mapped the shared inner space between the two objects—the wormhole connecting them. They found that for a typical, messy entangled pair, the interior isn’t the smooth tunnel of science fiction.
Instead, it’s a long, lumpy structure they called the “Einstein-Rosen caterpillar.” It’s named after the Einstein-Rosen Bridge, the mathematical structure that connects two regions of spacetime, and “caterpillar” because of its bumpy, segmented shape. This discovery is a significant step toward proving that the bizarre rules of quantum mechanics can control the shape of spacetime inside a black hole.

🌌 Unifying AI Through the Feynman Path Integral: From Deep Learning to Quantum AI https://lnkd.in/g4Cfv6qd I’m pleased to share a framework that brings many areas of AI into a single mathematical structure inspired by the Feynman path integral — a foundational idea in quantum physics. Instead of viewing supervised learning, reinforcement learning, generative models, and quantum machine learning as separate disciplines, this framework shows that they all follow the same underlying principle: Learning is a weighted sum over possible solutions (paths), based on how well each one explains the data. In other words, AI can be viewed the same way Feynman viewed physics: as summing over all possible configurations, weighted by an action functional.

Researchers at the University of Warwick have created a straightforward new way to predict how irregularly shaped nanoparticles, a harmful type of airborne pollutant, move through the air.
Each day, people inhale countless microscopic particles such as soot, dust, pollen, microplastics, viruses, and engineered nanoparticles. Many of these particles are so small that they can reach deep into the lungs and even pass into the bloodstream, where they may contribute to serious health problems including heart disease, stroke, and cancer.
While most airborne particles have uneven shapes, existing mathematical models often treat them as perfect spheres because that makes the equations easier to handle. This simplification limits scientists’ ability to accurately describe or track how real, non-spherical particles move, especially those that are more dangerous.