A brain cap and smart algorithms may one day help paralyzed patients turn thought into movement—no surgery required.


Artificial intelligence (AI) is said to be a “black box,” with its logic obscured from human understanding—but how much does the average user actually care to know how AI works?
It depends on the extent to which a system meets users’ expectations, according to a new study by a team that includes Penn State researchers. Using a fabricated algorithm-driven dating website, the team found that whether the system met, exceeded or fell short of user expectations directly corresponded to how much the user trusted the AI and wanted to know about how it worked.
The findings are published in the journal Computers in Human Behavior.
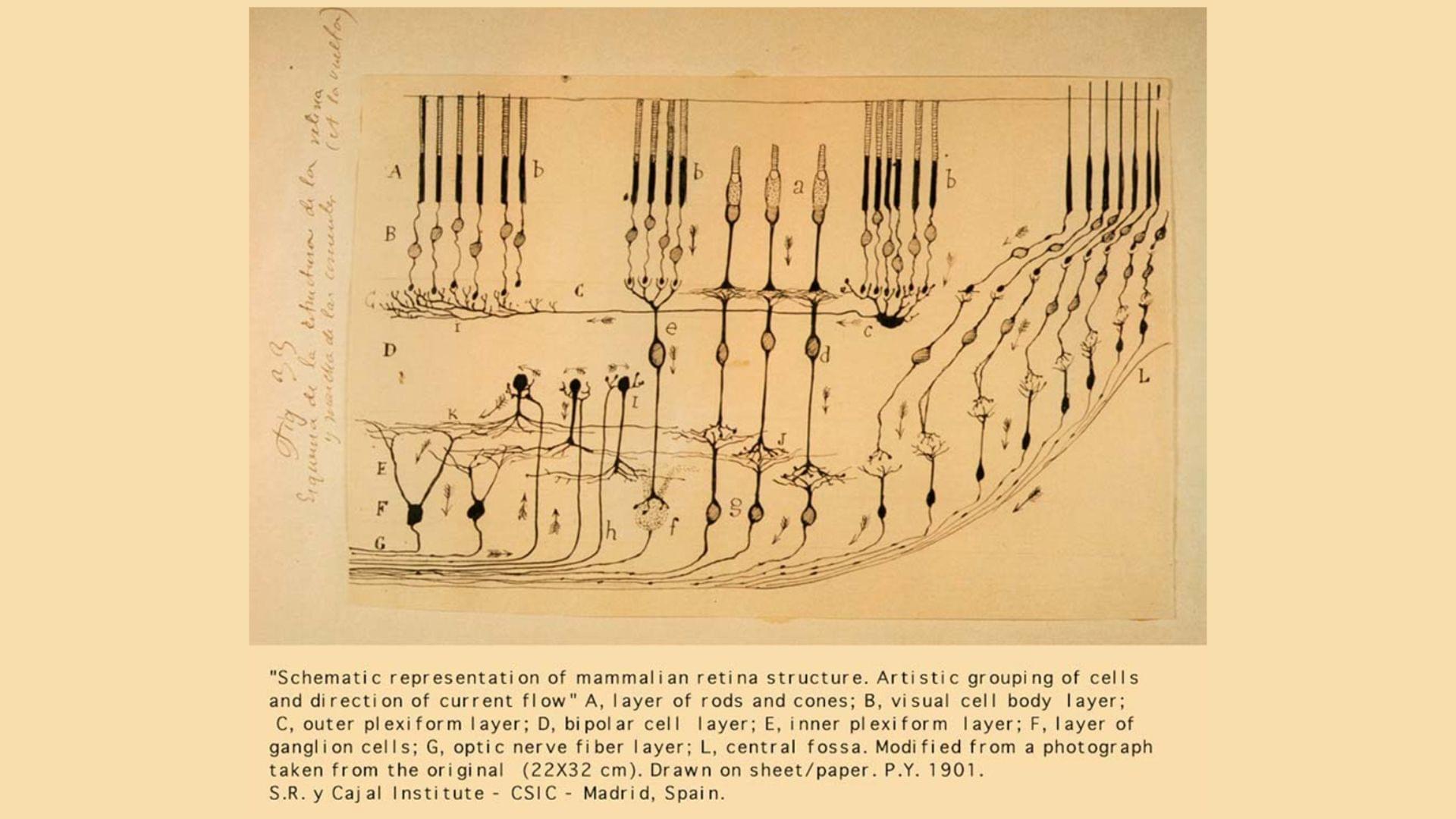
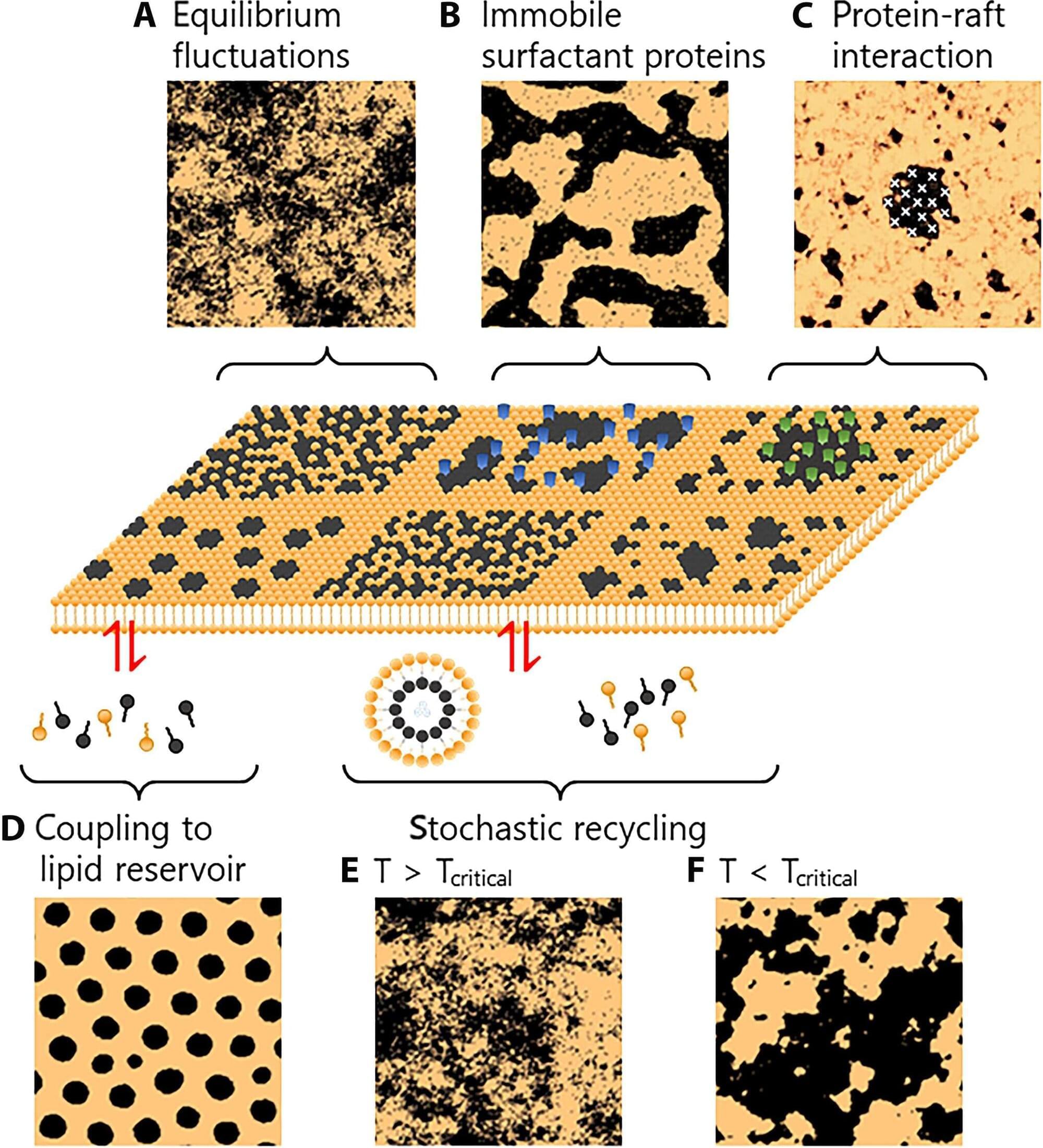
A collaborative team of four professors and several graduate students from the Departments of Chemistry and Biochemical Science and Technology at National Taiwan University, together with the Department of Applied Chemistry at National Chi Nan University, has achieved a long-sought breakthrough.
By combining atomic force microscopy (AFM) with a Hadamard product–based image reconstruction algorithm, the researchers successfully visualized, for the first time, the nanoscopic dynamics of membrane rafts in live cells—making visible what had long remained invisible on the cell membrane.
Membrane rafts are nanometer-scale structures rich in cholesterol and sphingolipids, believed to serve as vital platforms for cell signaling, viral entry, and cancer metastasis. Since the concept emerged in the 1990s, the existence and behavior of these lipid domains have been intensely debated.
When we talk about the universe, we usually imagine space filled with galaxies, stars, and matter expanding endlessly in all directions. It feels natural to think of the universe as a vast container — a place where everything exists. But modern theoretical physics suggests that this picture may be deeply misleading.
In this video, we explore a more fundamental question: what is the universe really made of? Is it space? Matter? Energy? Or something far more abstract than our everyday intuition allows?
Drawing on ideas associated with Leonard Susskind, this long-form exploration challenges the assumption that the universe is a physical stage where reality takes place. Instead, physics increasingly points toward a universe defined not by objects and locations, but by information, relationships, and boundaries.
Black hole physics, quantum theory, and modern cosmology have forced scientists to rethink the foundations of reality. In some of the deepest descriptions of nature, space and time no longer appear as fundamental ingredients. What we experience as a three-dimensional universe may be an emergent structure — a convenient description rather than the true underlying reality.
Rather than focusing on equations, this video emphasizes intuition and conceptual understanding. Through thought experiments and simple analogies, we examine why the universe feels like a place, why that picture works so well at human scales, and why it may break down at the most fundamental level.

This is the second time in recent months that the AI world has got all excited about math. The rumor mill went into overdrive last November, when there were reports that the boardroom drama at OpenAI, which saw CEO Sam Altman temporarily ousted, was caused by a new powerful AI breakthrough. It was reported that the AI system in question was called Q* and could solve complex math calculations. (The company has not commented on Q*, and we still don’t know if there was any link to the Altman ouster or not.) I unpacked the drama and hype in this story.
You don’t need to be really into math to see why this stuff is potentially very exciting. Math is really, really hard for AI models. Complex math, such as geometry, requires sophisticated reasoning skills, and many AI researchers believe that the ability to crack it could herald more powerful and intelligent systems. Innovations like AlphaGeometry show that we are edging closer to machines with more human-like reasoning skills. This could allow us to build more powerful AI tools that could be used to help mathematicians solve equations and perhaps come up with better tutoring tools.
(June 13, 1928 – May 23, 2015), known and published as John Nash, was an American mathematician who made fundamental contributions to game theory, real algebraic geometry, differential geometry, and partial differential equations. [ 1 ] [ 2 ] Nash and fellow game theorists John Harsanyi and Reinhard Selten were awarded the 1994 Nobel Prize in Economics. [ 3 ] In 2015, Louis Nirenberg and he were awarded the Abel Prize for their contributions to the field of partial differential equations.
As a graduate student in the Princeton University Department of Mathematics, Nash introduced a number of concepts (including the Nash equilibrium and the Nash bargaining solution), which are now considered central to game theory and its applications in various sciences. In the 1950s, Nash discovered and proved the Nash embedding theorems by solving a system of nonlinear partial differential equations arising in Riemannian geometry. This work, also introducing a preliminary form of the Nash–Moser theorem, was later recognized by the American Mathematical Society with the Leroy P. Steele Prize for Seminal Contribution to Research. Ennio De Giorgi and Nash found, with separate methods, a body of results paving the way for a systematic understanding of elliptic and parabolic partial differential equations.
The Age of Abundance: AGI Predictions and Investment Strategy for 2026 ## The imminent emergence of Artificial General Intelligence (AGI) will significantly impact investment strategies, and investors should prepare by accumulating valuable assets, diversifying their portfolios, and adopting a strategic investment approach to capitalize on the growth potential of AGI and the resulting Age of Abundance ##
## Questions to inspire discussion.
Investment Strategy.
🎯 Q: How should I build an investment portfolio for the AGI era? A: Focus on companies with best management and growth potential in AGI, robotics, and space industries using dollar-cost averaging strategy to systematically build positions over time rather than lump-sum investing.
💰 Q: What alternative assets should I accumulate for security during AGI transition? A: Accumulate gold, silver, and Bitcoin as modern safe havens to protect wealth during periods of change and uncertainty as traditional financial systems adapt to AGI disruption.
🏢 Q: Why should real estate be overweighted in an AGI-focused portfolio? A: Overweight real estate compared to company ownership and reserves because AGI and robotics industries will require physical space for operations, data centers, and manufacturing facilities.

The advancement of artificial intelligence (AI) algorithms has opened new possibilities for the development of robots that can reliably tackle various everyday tasks. Training and evaluating these algorithms, however, typically requires extensive efforts, as humans still need to manually label training data and assess the performance of models in both simulations and real-world experiments.
Researchers at Stanford University and UC Berkeley have introduced RoboReward, a dataset for training and evaluating AI algorithms for robotics applications, specifically vision-language reward-based models (VLMs).
Their paper, published on the arXiv preprint server, also presents RoboReward 4B and 8B, two new VLMs that were trained on this dataset and outperform other models introduced in the past.
