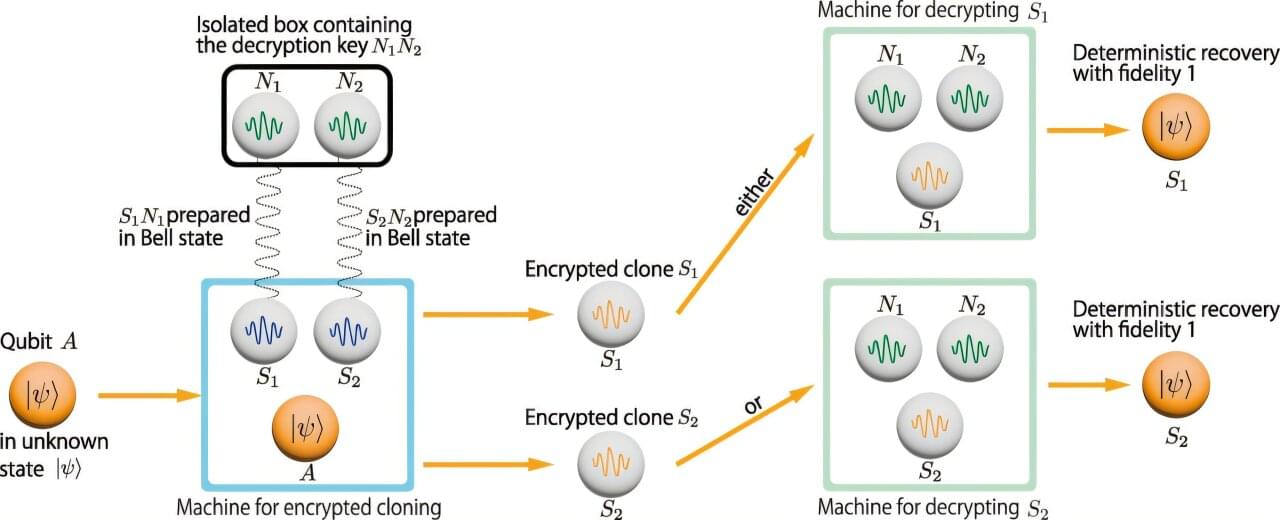
Quantum key distribution (QKD) is a next generation method for protecting digital communications by drawing on the fundamental behavior of quantum particles. Instead of relying on mathematical complexity alone, QKD allows two users to establish a shared secret key in a way that is inherently resistant to interception, even if the communication channel itself is not private.
When an unauthorized observer attempts to extract information, the quantum states carrying the data are unavoidably altered, creating telltale disturbances that signal a potential security breach.
The real-world performance of QKD systems, however, depends on precise control of the physical link between sender and receiver. One of the most influential factors is pointing error, which occurs when the transmitted beam does not perfectly align with the receiving device.