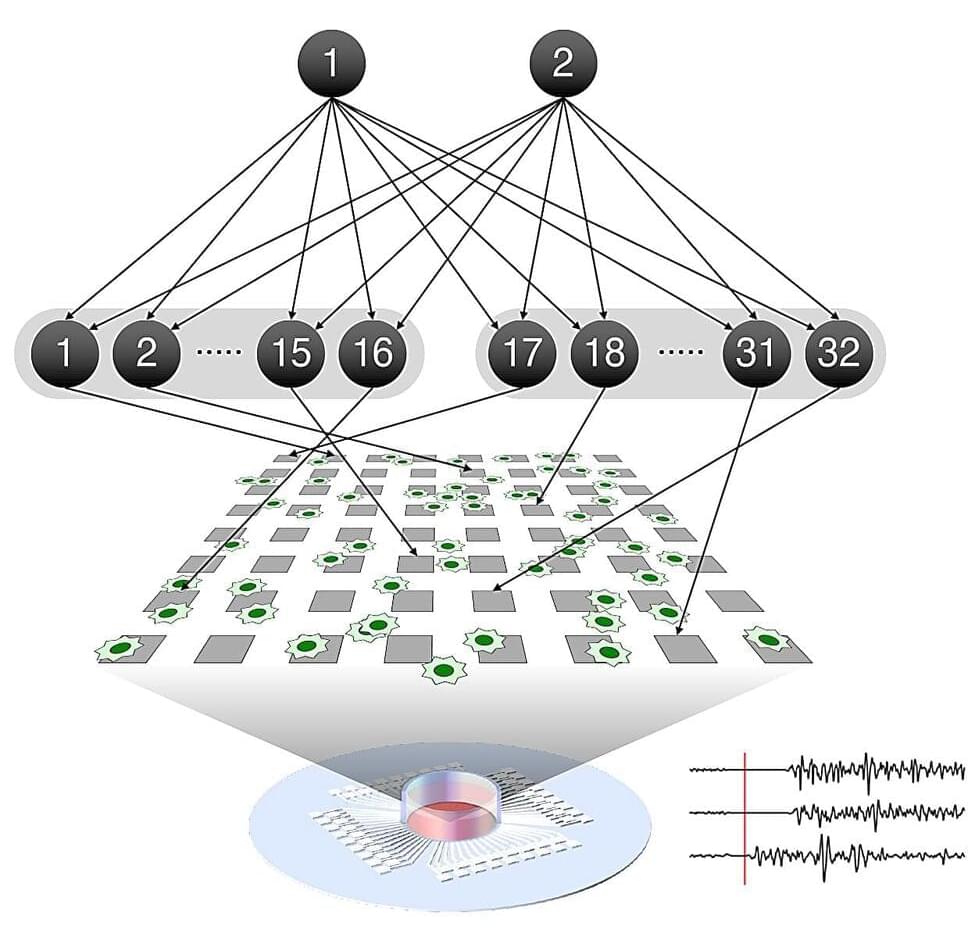
An international collaboration between researchers at the RIKEN Center for Brain Science (CBS) in Japan, the University of Tokyo, and University College London has demonstrated that self-organization of neurons as they learn follows a mathematical theory called the free energy principle.
The principle accurately predicted how real neural networks spontaneously reorganize to distinguish incoming information, as well as how altering neural excitability can disrupt the process. The findings thus have implications for building animal-like artificial intelligences and for understanding cases of impaired learning. The study was published August 7 in Nature Communications.
When we learn to tell the difference between voices, faces, or smells, networks of neurons in our brains automatically organize themselves so that they can distinguish between the different sources of incoming information. This process involves changing the strength of connections between neurons, and is the basis of all learning in the brain.