If you look across space with a telescope, you’ll see countless galaxies, most of which host large central black holes, billions of stars and their attendant planets. The universe teems with huge, spectacular objects, and it might seem like these massive objects should hold most of the universe’s matter.
But the Big Bang theory predicts that about 5% of the universe’s contents should be atoms made of protons, neutrons and electrons. Most of those atoms cannot be found in stars and galaxies—a discrepancy that has puzzled astronomers.
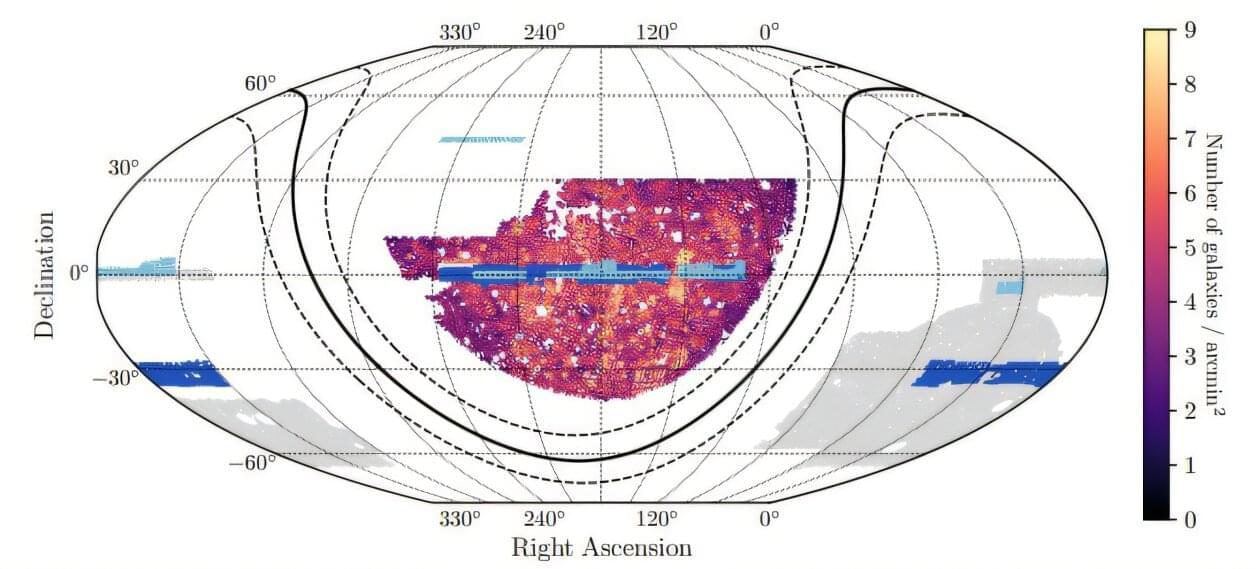
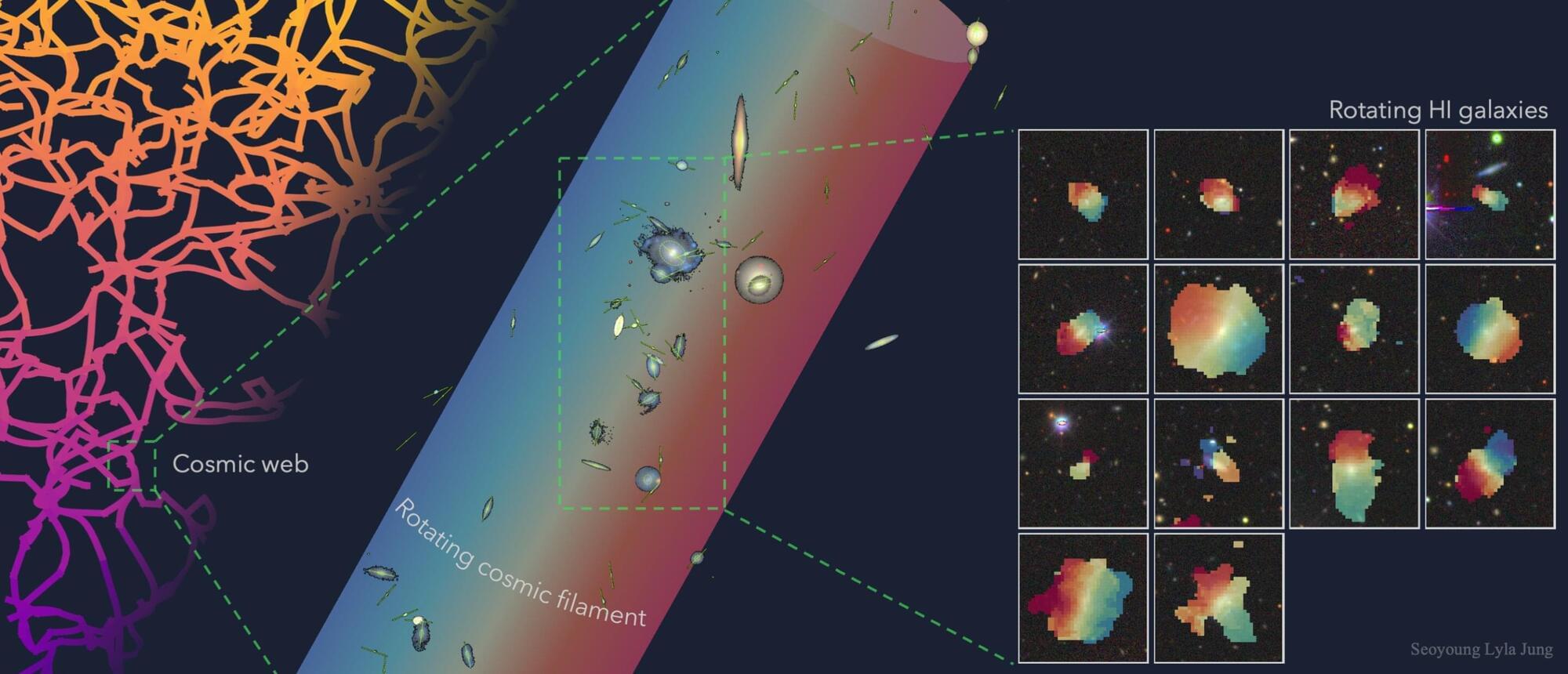
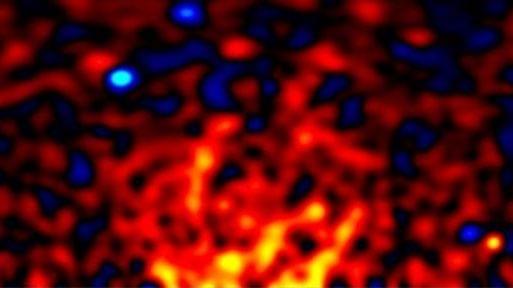
If not in visible stars and galaxies, the most likely hiding place for the matter is in the dark space between galaxies. While space is often referred to as a vacuum, it isn’t completely empty. Individual particles and atoms are dispersed throughout the space between stars and galaxies, forming a dark, filamentary network called the “cosmic web.”