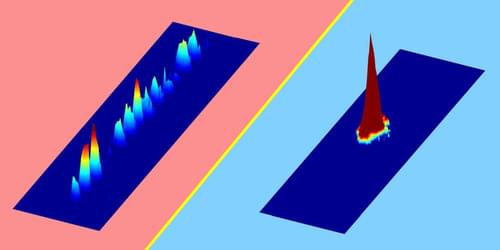
A cold-atom experiment suggests that interactions between particles can induce the coexistence of localized and extended states in a quantum wire.

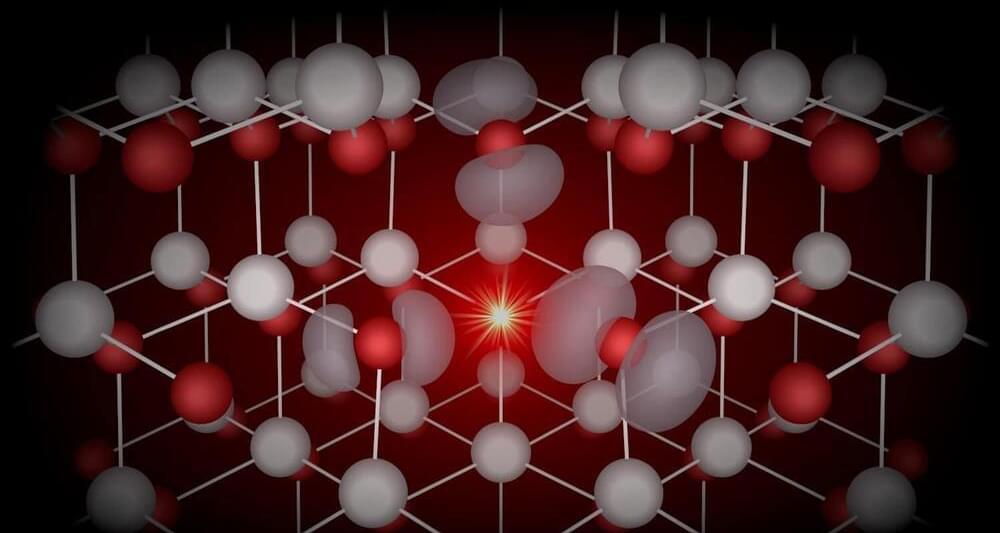
Researchers from North Carolina State University used computational analysis to predict how optical properties of semiconductor material zinc selenide (ZnSe) change when doped with halogen elements, and found the predictions were confirmed by experimental results. Their method could speed the process of identifying and creating materials useful in quantum applications.
Creating semiconductors with desirable properties means taking advantage of point defects—sites within a material where an atom may be missing, or where there are impurities. By manipulating these sites in the material, often by adding different elements (a process referred to as “doping”), designers can elicit different properties.
“Defects are unavoidable, even in ‘pure’ materials,” says Doug Irving, University Faculty Scholar and professor of materials science and engineering at NC State. “We want to interface with those spaces via doping to change certain properties of a material. But figuring out which elements to use in doping is time and labor intensive. If we could use a computer model to predict these outcomes it would allow material engineers to focus on elements with the best potential.”

Japanese and U.S. physicists have used atoms about 3 billion times colder than interstellar space to open a portal to an unexplored realm of quantum magnetism.
“Unless an alien civilization is doing experiments like these right now, anytime this experiment is running at Kyoto University it is making the coldest fermions in the universe,” said Rice University’s Kaden Hazzard, corresponding theory author of a study published today in Nature Physics. “Fermions are not rare particles. They include things like electrons and are one of two types of particles that all matter is made of.”
A Kyoto team led by study author Yoshiro Takahashi used lasers to cool its fermions, atoms of ytterbium, within about one-billionth of a degree of absolute zero, the unattainable temperature where all motion stops. That’s about 3 billion times colder than interstellar space, which is still warmed by the afterglow from the Big Bang.
Researchers have discovered a new method for correcting errors in the calculations of quantum computers, potentially clearing a major obstacle to a powerful new realm of computing.
In conventional computers, fixing errors is a well-developed field. Every cellphone requires checks and fixes to send and receive data over messy airwaves. Quantum computers offer enormous potential to solve certain complex problems that are impossible for conventional computers, but this power depends on harnessing extremely fleeting behaviors of subatomic particles. These computing behaviors are so ephemeral that even looking in on them to check for errors can cause the whole system to collapse.
In a paper outlining a new theory for error correction, published Aug. 9 in Nature Communications, an interdisciplinary team led by Jeff Thompson, an associate professor of electrical and computer engineering at Princeton, and collaborators Yue Wu and Shruti Puri at Yale University and Shimon Kolkowitz at the University of Wisconsin-Madison, showed that they could dramatically improve a quantum computer’s tolerance for faults, and reduce the amount of redundant information needed to isolate and fix errors. The new technique increases the acceptable error rate four-fold, from 1% to 4%, which is practical for quantum computers currently in development.

While having their own unique areas of expertise and resources, the NQISRCs are all aligned to the same mission—the advancement of quantum information science.
Five National Quantum Information Science Research Centers (NQISRCs) are leveraging the behavior of nature at the smallest scales to develop technologies for science’s most complex problems. Supported by the U.S. Department of Energy (DOE) Office of Science, the NQISRCs have been supporting DOE’s mission since 2020 to advance the energy, economic and national security of the United States. By building a national quantum ecosystem and workforce comprising researchers at roughly 70 institutions across the United States, the centers create a rich environment for quantum innovation and co-design.
The NQISRCs integrate state-of-the-art DOE facilities, preeminent talent at national laboratories and U.S. universities, and the enterprising ingenuity of U.S. technology companies.

Qubits are the building blocks of quantum computers, which have the potential to revolutionize many fields of research by solving problems that classical computers can’t.
But creating qubits that have the perfect quality necessary for quantum computing can be challenging.
Researchers at the University of Wisconsin–Madison, HRL Laboratories LLC, and University of New South Wales (UNSW) collaborated on a project to better control silicon quantum dot qubits, allowing for higher-quality fabrication and use in wider applications. All three institutions are affiliated with the Chicago Quantum Exchange.

Qubits are the building blocks of quantum computers, which have the potential to revolutionize many fields of research by solving problems that classical computers can’t.
But creating qubits that have the perfect quality necessary for quantum computing can be challenging.
Researchers at the University of Wisconsin–Madison, HRL Laboratories LLC, and University of New South Wales (UNSW) collaborated on a project to better control silicon quantum dot qubits, allowing for higher-quality fabrication and use in wider applications. All three institutions are affiliated with the Chicago Quantum Exchange. The work was published in Physical Review Letters, and the lead author, J. P. Dodson, has recently transitioned from UW–Madison to HRL.
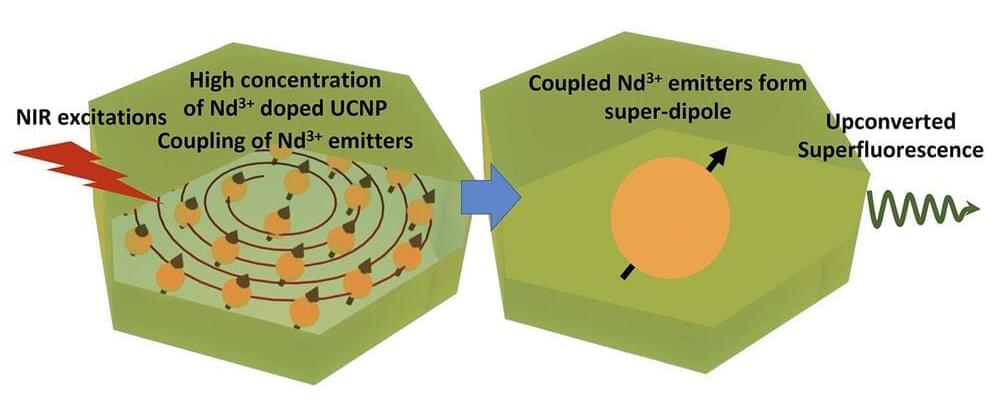
Researchers looking to synthesize a brighter and more stable nanoparticle for optical applications found that their creation instead exhibited a more surprising property: bursts of superfluorescence that occurred at both room temperature and regular intervals. The work could lead to the development of faster microchips, neurosensors, or materials for use in quantum computing applications, as well as a number of biological studies.
Superfluorescence occurs when atoms within a material synchronize and simultaneously emit a short but intense burst of light. The property is valuable for quantum optical applications, but extremely difficult to achieve at room temperatures and for intervals long enough to be useful.
The material in question—lanthanide-doped upconversion nanoparticle, or UCNP—was synthesized by the research team in an effort to create a “brighter” optical material. They produced hexagonal ceramic crystals ranging from 50 nanometers (nm) to 500 nm in size and began testing their lasing properties, which resulted in several impressive breakthroughs.

Aug. 24, 2022 — Training a quantum neural network requires only a small amount of data, according to a new proof that upends previous assumptions stemming from classical computing’s huge appetite for data in machine learning, or artificial intelligence. The theorem has several direct applications, including more efficient compiling for quantum computers and distinguishing phases of matter for materials discovery.
“Many people believe that quantum machine learning will require a lot of data. We have rigorously shown that for many relevant problems, this is not the case,” said Lukasz Cincio, a quantum theorist at Los Alamos National Laboratory and co-author of the paper containing the proof published in the journal Nature Communications. “This provides new hope for quantum machine learning. We’re closing the gap between what we have today and what’s needed for quantum advantage, when quantum computers outperform classical computers.”
“The need for large data sets could have been a roadblock to quantum AI, but our work removes this roadblock. While other issues for quantum AI could still exist, at least now we know that the size of the data set is not an issue,” said Patrick Coles, a quantum theorist at the Laboratory and co-author of the paper.