A concept based on an exotic effect in periodic structures may be useful for developing future photonic devices.
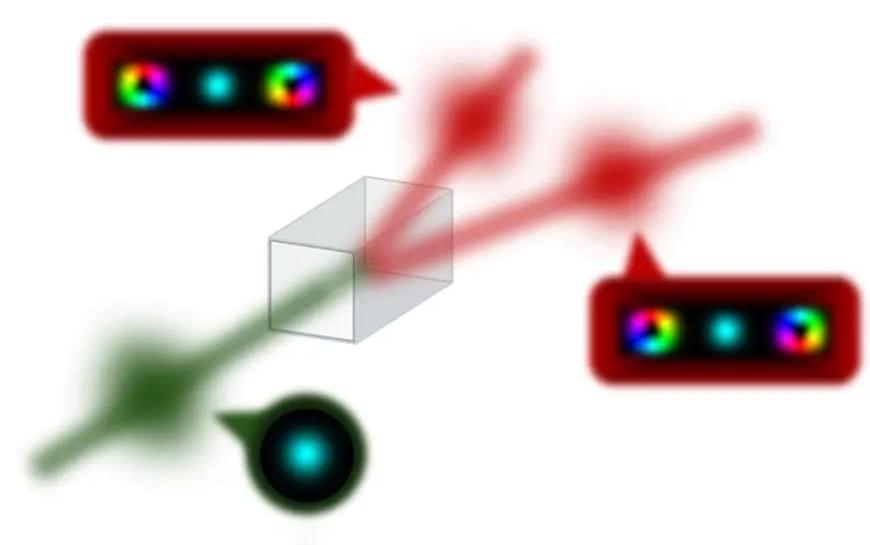
A new way to marshal light within optical devices has been demonstrated experimentally by researchers in China. They have been able to induce light to organize itself into specific patterns of pulses as it circulates within a pair of optical fiber loops using a version of a phenomenon—called the non-Hermitian skin effect (NHSE)—that has been predicted but not observed previously [1]. The effect could be used to control light signals in photonic devices such as switches and routers.
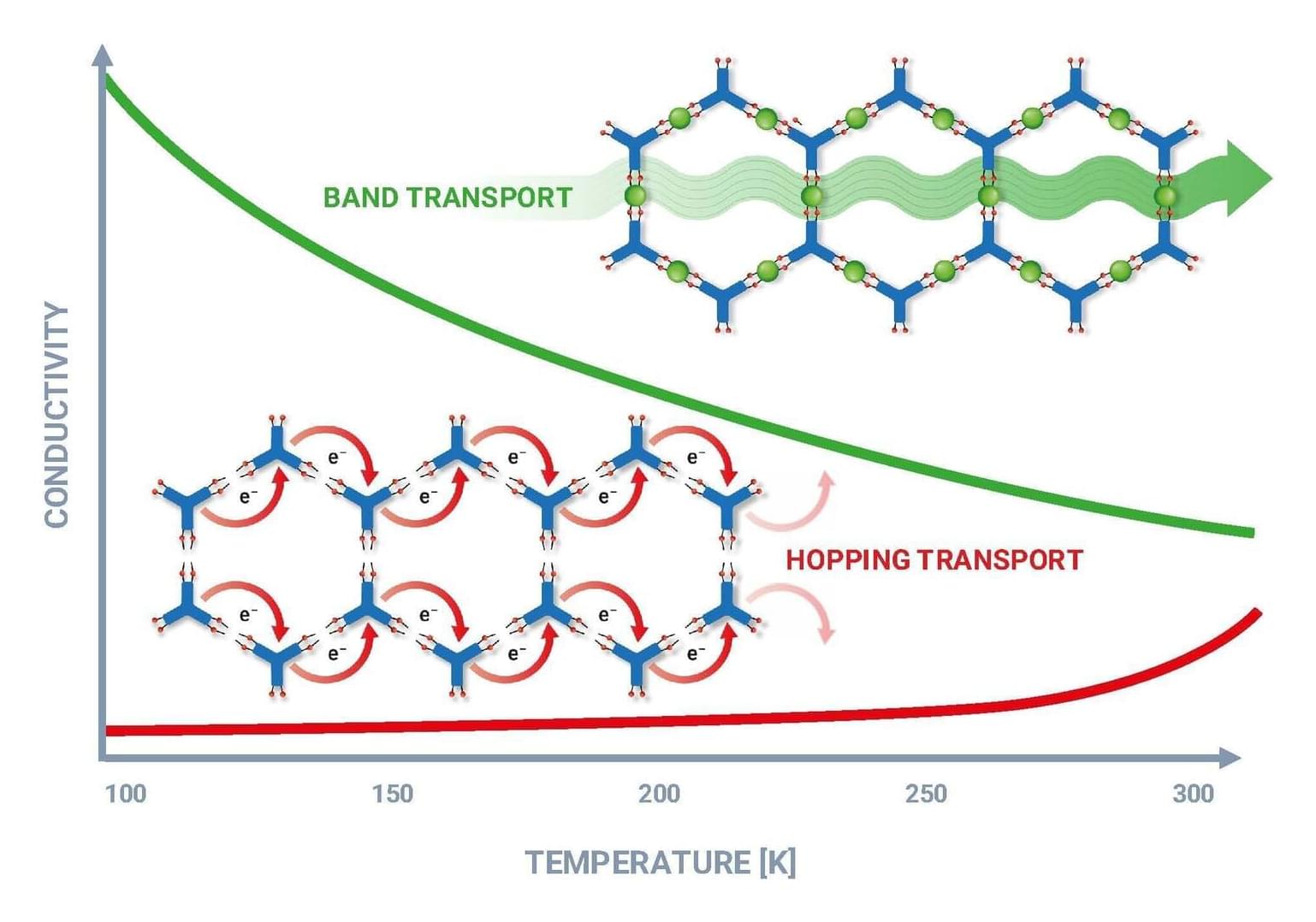
In the standard theory for electron behavior in a metallic crystal, the periodic atomic structure leads to so-called Bloch waves—electron quantum states that spread across the entire crystal. But in recent years, theorists have found surprising results for a scenario in which one assumes that a particle such as an electron hops between neighboring sites in a periodic lattice asymmetrically—say, rightward hopping is more probable than leftward hopping. The particle’s quantum states become localized at the edge or surface of the lattice rather than spreading across it. This localization is the NHSE.