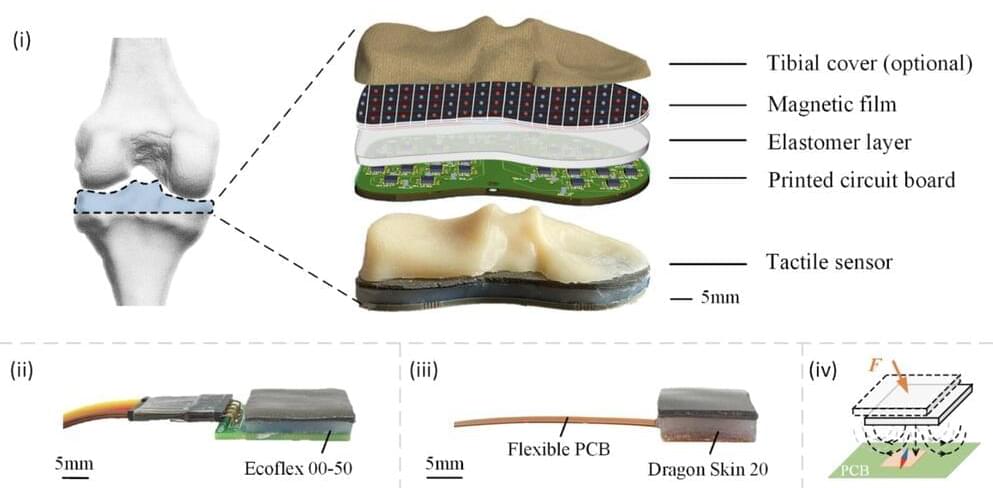
Cellular death is a fundamental concept in biological sciences. Despite its importance, its definition varies depending on the context in which it occurs and lacks a general mathematical definition.
Researchers from the University of Tokyo propose a new mathematical definition of death based on whether a potentially dead cell can return to a predefined “representative state of living,” which are the states of being that we can confidently call “alive.” The researchers’ work could be useful for biological researchers and future medical research.
While it’s not something we like to think about, death comes for us all eventually, whether you’re an animal, a plant, or even a cell. And even though we can all differentiate between what is alive and dead, it might be surprising to know that death at a cellular level lacks a widely recognized mathematical definition.