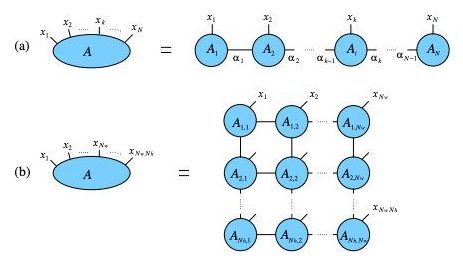
Quantum many-body systems (QMBs), which are physical systems made up of multiple interacting particles, are among the most challenging structures to reproduce in numerical simulations. In the past, researchers have attempted to simulate these systems using a variety of techniques, including Monte Carlo simulations and even exact diagonalizations.
Methods involving tensor networks (TNs), mathematical concepts that can be applied in a variety of scientific fields, have also shown some potential for the simulation of QMBs. However, so far, these techniques have only been successfully applied to small systems or those with a simple geometry.
In a recent study, researchers at the University of Central Florida were able to simulate QMBs on Amazon Web Services using a TN-based method. Their paper, pre-published on arXiv, highlights some of the potential advantages and implications of using cloud services for research purposes.



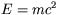 says that mass of a particle determines the energy of the particle at rest. For an electron, its rest energy is known to be 0.511 MeV. For this given amount of energy, it cannot afford to “pack” itself into a size smaller than the size of a nucleus. Classical theory of electromagnetism is not a consistent theory below this distance. However, it is known that the electron is at least ten thousand times smaller than that.
says that mass of a particle determines the energy of the particle at rest. For an electron, its rest energy is known to be 0.511 MeV. For this given amount of energy, it cannot afford to “pack” itself into a size smaller than the size of a nucleus. Classical theory of electromagnetism is not a consistent theory below this distance. However, it is known that the electron is at least ten thousand times smaller than that.