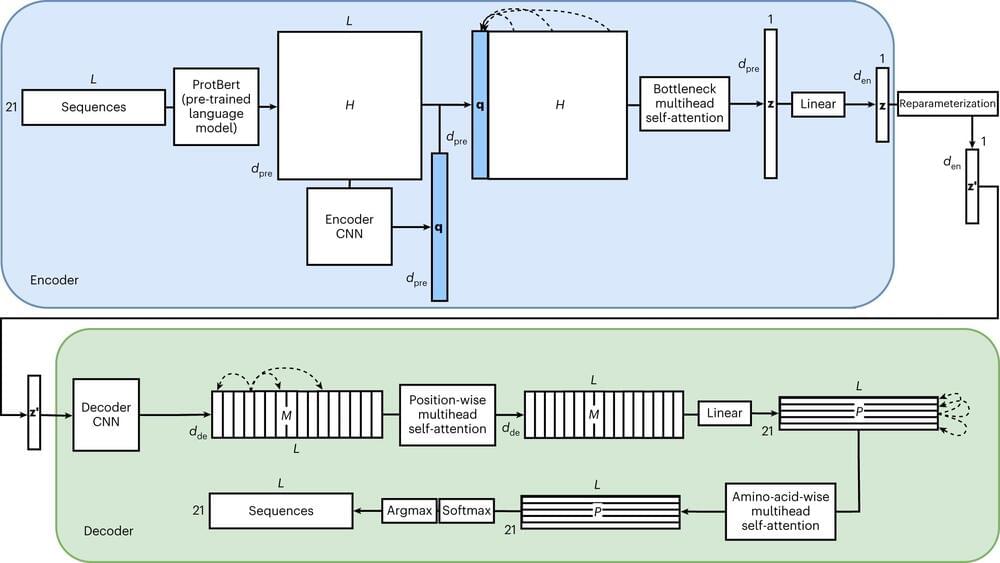
Researchers at the University of Toronto have used an artificial intelligence framework to redesign a crucial protein involved in the delivery of gene therapy.
The study, published in Nature Machine Intelligence, describes new work optimizing proteins to mitigate immune responses, thereby improving the efficacy of gene therapy and reducing side effects.
“Gene therapy holds immense promise, but the body’s pre-existing immune response to viral vectors greatly hampers its success. Our research zeroes in on hexons, a fundamental protein in adenovirus vectors, which—but for the immune problem—hold huge potential for gene therapy,” says Michael Garton, an assistant professor at the Institute of Biomedical Engineering in the Faculty of Applied Science & Engineering.