Tiny particles are interconnected despite sometimes being thousands of kilometers apart—Albert Einstein called this “spooky action at a distance.” Something that would be inexplicable by the laws of classical physics is a fundamental part of quantum physics. Entanglement like this can occur between multiple quantum particles, meaning that certain properties of the particles are intimately linked with each other.
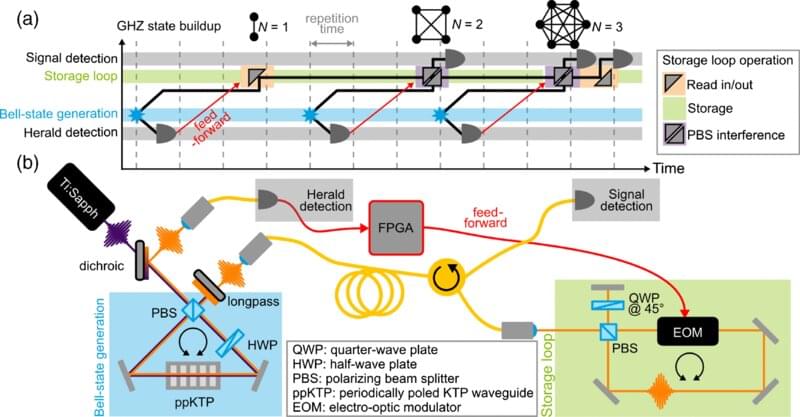
Entangled systems containing multiple quantum particles offer significant benefits in implementing quantum algorithms, which have the potential to be used in communications, data security or quantum computing. Researchers from Paderborn University have been working with colleagues from Ulm University to develop the first programmable optical quantum memory. The study was published as an “Editor’s suggestion” in the Physical Review Letters journal.