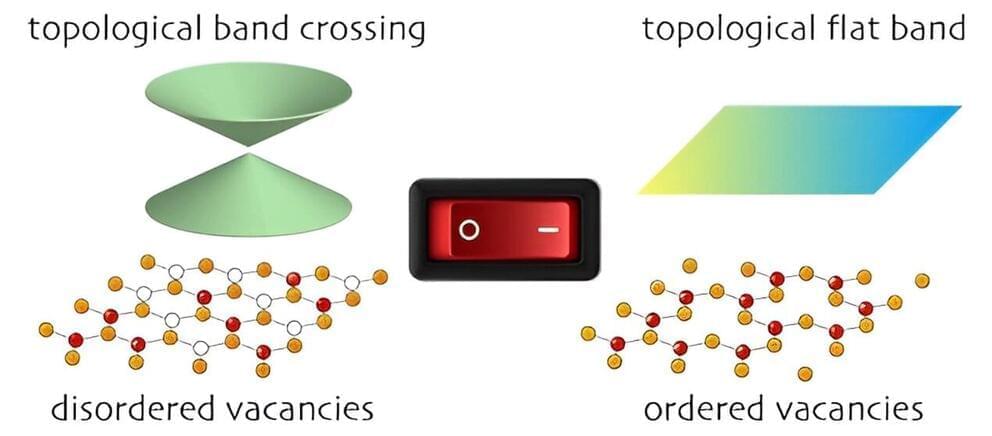
When looking into the future, there are a number of interesting trends, such as quantum computing, which may save lots of energy, or space travel, which is here to stay and will become more affordable. But what I find interesting is the development of computation with biological cells, and the ability to build computing systems, and robots, not from hard metals but from soft biological matter — mostly cells.
Look around you in “nature”- almost everything you see, all plants and animals are built from a single type of structure, a biological cell. They are all alike. Sure, cells vary as they adapt to their environments, but a cellular organism has the same building plan as any other cell. There’s the cell membrane, there is a nucleus, there are organelles and cytoplasm. There is DNA, RNA, amino acids to build proteins and peptides, lipids and sugars. Put together in predictable ways.
We are learning to use these systems to build anything we want from them. We focus on this because our bodies are made from cells, and we want to remain healthy. That is a strong incentive to study these systems. The convergence will happen when we relegate metal-based computing to the sidelines and focus on biological computing as our main systems. These biological cell systems are, incidentally, quantum computing systems. So the trends I mention — here on earth will converge, and only space travel will require the opposite — the need to shield biological computing from conditions in space.