If the firm can demonstrate superior returns through its AI-first approach, it could accelerate similar transformations across the industry.


Artificial intelligence (AI) agents and large-language models (LLMs), such as the model underpinning OpenAI’s conversational platform ChatGPT, are now widely used by people worldwide, both in informal and professional settings. Over the past decade or so, some of these models have also been adapted to tackle complex research problems rooted in various fields, including biology, physics, medical sciences and chemistry.
Existing computational tools employed by chemists are often highly sophisticated and complex. Their complexity makes them inaccessible to non-expert users and often even difficult for expert chemists to use.
Researchers at Matter Lab at the University of Toronto and NVIDIA have developed El Agente Q, a new LLM-based system that could allow chemists, particularly those specialized in quantum chemistry, to easily generate and execute quantum chemistry workflows, sequences of computational tasks required to study specific chemical systems at the quantum mechanical level.
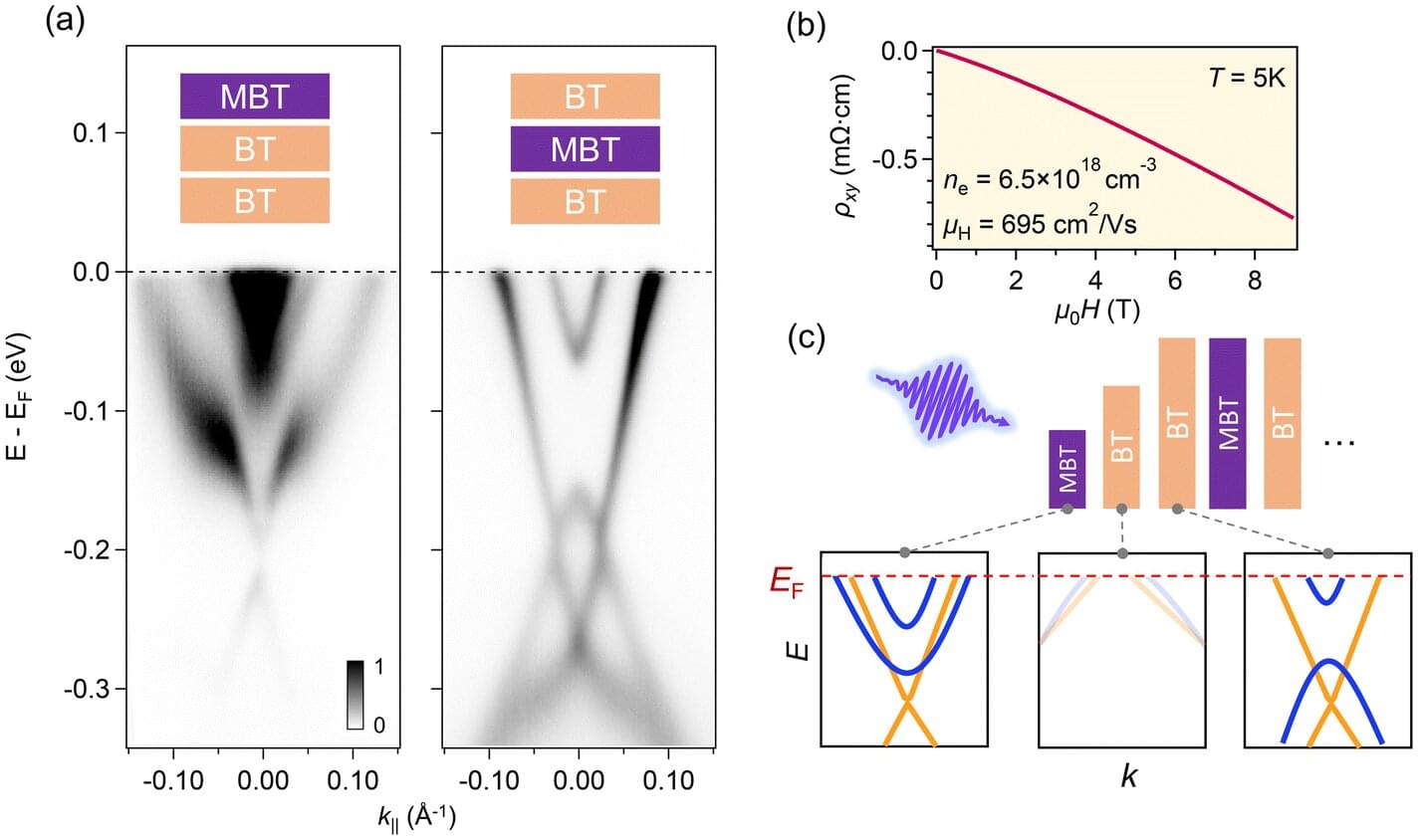
Scientists studying a promising quantum material have stumbled upon a surprise: within its crystal structure, the material naturally forms one of the world’s thinnest semiconductor junctions—a building block of most modern electronics. The junction is just 3.3 nanometers thick, about 25,000 times thinner than a sheet of paper.
“This was a big surprise,” said Asst. Prof. Shuolong Yang. “We weren’t trying to make this junction, but the material made one on its own, and it’s one of the thinnest we’ve ever seen.”
The discovery offers a way to build ultra-miniaturized electronic components, and also provides insight into how electrons behave in materials designed for quantum applications.
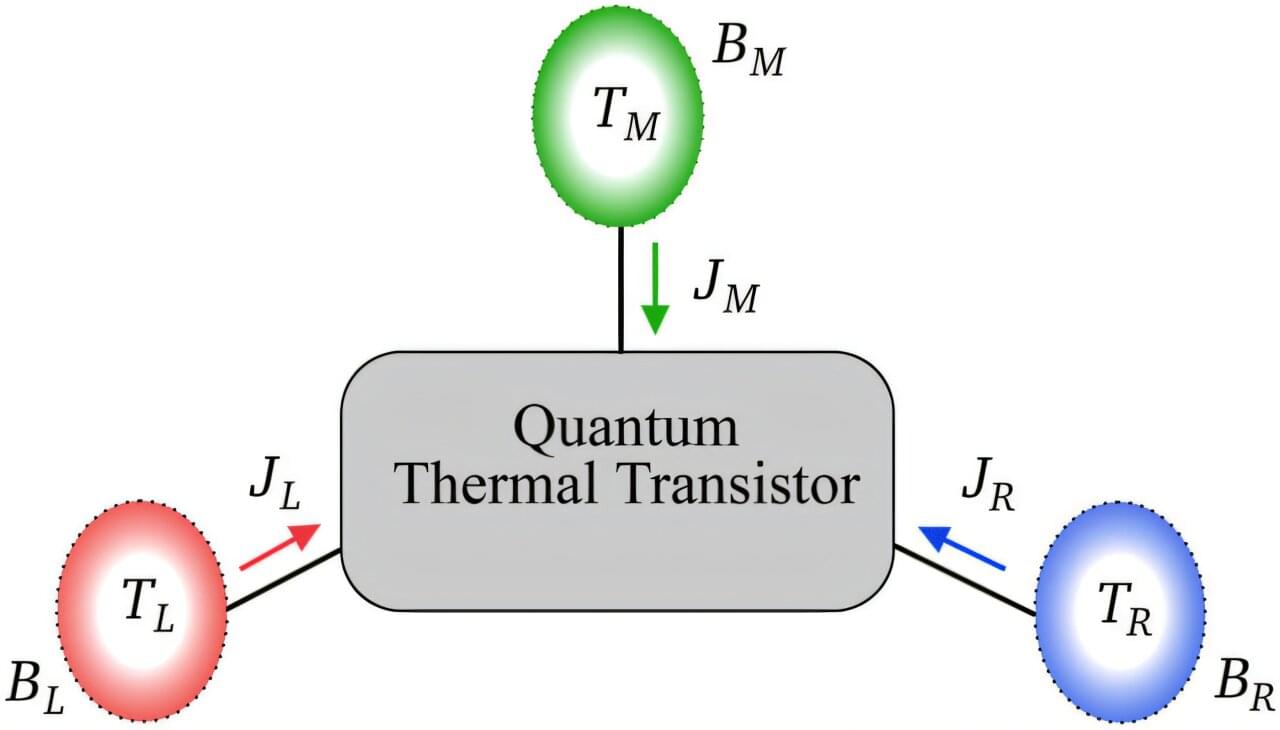
Transistors are the fundamental building blocks behind today’s electronic revolution, powering everything from smartphones to powerful servers by controlling the flow of electrical currents. But imagine a parallel world, where we could apply the same level of control and sophistication—not to electricity, but to heat.
This is precisely the frontier being explored through quantum thermal transistors, devices designed to replicate electronic transistor functionality at the quantum scale, but for heat.
The rapidly growing field of quantum thermodynamics has been making impressive strides, exploring how heat and energy behave when quantum mechanical effects dominate. Innovations such as quantum thermal diodes, capable of directing heat flow in a specific direction, and quantum thermal transistors, which amplify heat flows similarly to how electronic transistors amplify electric signals, are groundbreaking examples of this progress.
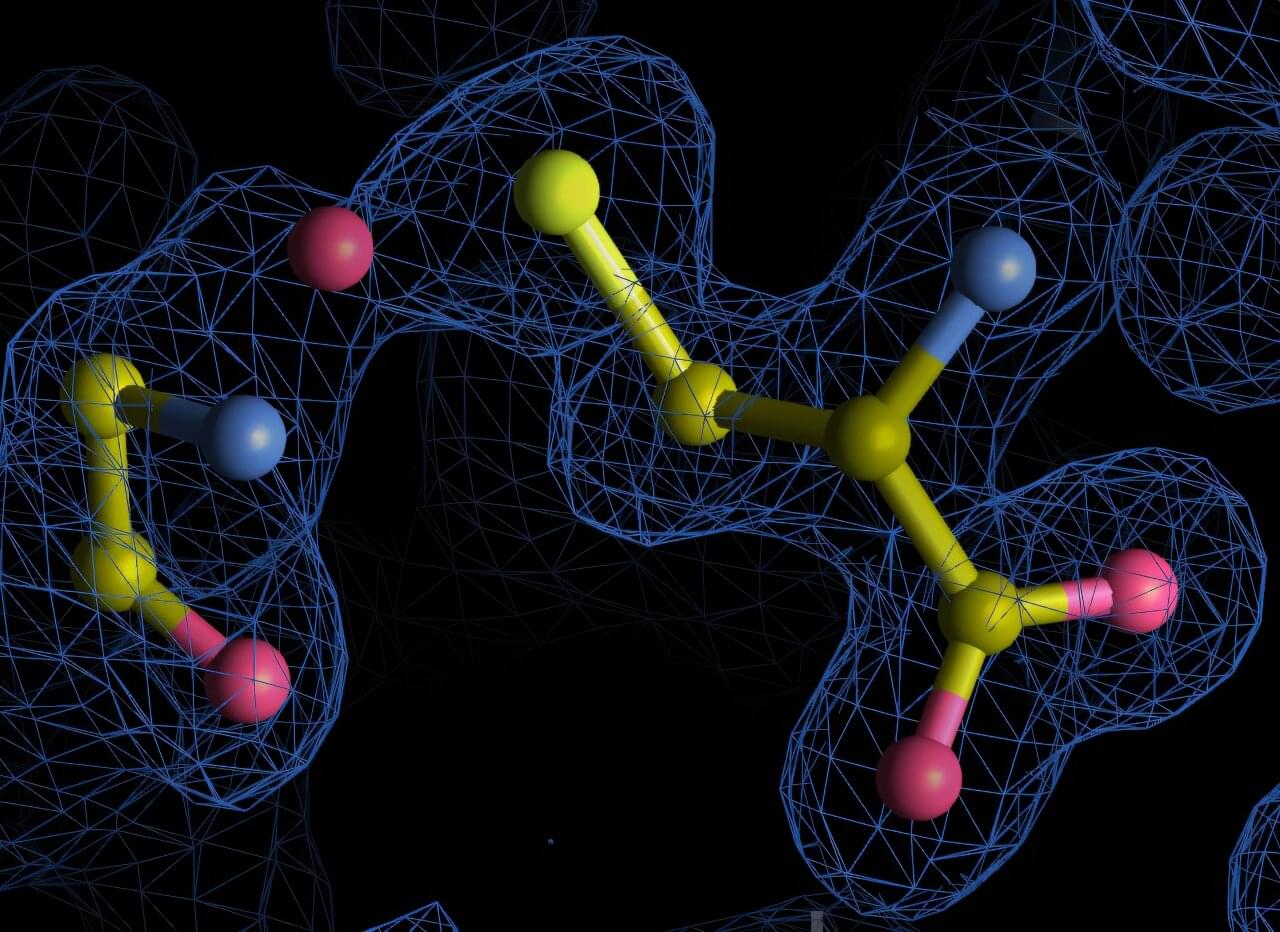
Proteins are among the most studied molecules in biology, yet new research from the University of Göttingen shows they can still hold surprising secrets. Researchers have discovered previously undetected chemical bonds within archived protein structures, revealing an unexpected complexity in protein chemistry.
These newly identified nitrogen-oxygen-sulfur (NOS) linkages broaden our understanding of how proteins respond to oxidative stress, a condition where harmful oxygen-based molecules build up and can damage proteins, DNA, and other essential parts of the cell. The new findings are published in Communications Chemistry.
The research team systematically re-analyzed over 86,000 high-resolution protein structures from the Protein Data Bank, a global public repository of protein structures, using a new algorithm that they developed inhouse called SimplifiedBondfinder. This pipeline combines machine learning, quantum mechanical modeling, and structural refinement methods to reveal subtle chemical bonds that were missed by conventional analyses.
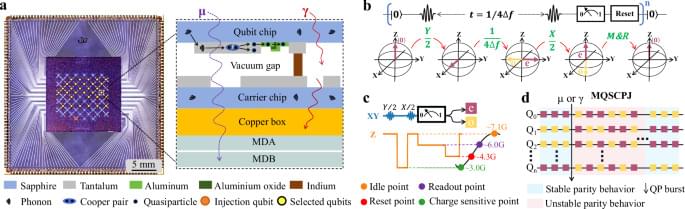
The correlated errors in superconducting qubits have been linked to high-energy particle impacts from cosmic rays, but a direct observation has been lacking. Here, the authors measure the quasiparticle bursts and correlated errors and separate the contributions of cosmic-ray muons and γ-rays in a 63-qubit processor.


The orbital angular momentum of electrons has long been considered a minor physical phenomenon, suppressed in most crystals and largely overlooked. Scientists at Forschungszentrum Jülich have now discovered that in certain materials it is not only preserved but can even be actively controlled. This is due to a property of the crystal structure called chirality, which also influences many other processes in nature.
The discovery has the potential to lead to a new class of electronic components capable of transmitting information with exceptional robustness and energy efficiency.
From electronics to spintronics, and now to orbitronics: In classical electronics, it is primarily the charge of the electron that counts. In modern approaches such as quantum computing and spintronics, the focus has shifted to the electron’s spin.
In a discovery that’s already turning heads in the scientific world, a team of physicists has achieved what was once thought impossible: they’ve measured the actual shape of a moving electron. This leap forward could not only reshape how we understand matter at the smallest scale—it might also unlock a new era of smarter, faster, and more energy-efficient electronics.