This is “OpenAI GPT-4o math with Sal and Imran Khan from Khan Academy” by OpenAI on Vimeo, the home for high quality videos and the people who love them.
Category: mathematics – Page 63
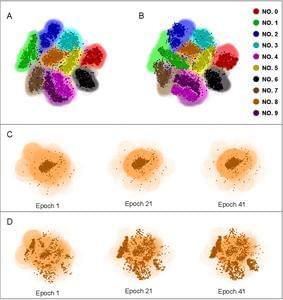
Scientists uncover quantum-inspired vulnerabilities in neural networks: the role of conjugate variables in system attacks
In a recent study merging the fields of quantum physics and computer science, Dr. Jun-Jie Zhang and Prof. Deyu Meng have explored the vulnerabilities of neural networks through the lens of the uncertainty principle in physics. Their work, published in the National Science Review, draws a parallel between the susceptibility of neural networks to targeted attacks and the limitations imposed by the uncertainty principle—a well-established theory in quantum physics that highlights the challenges of measuring certain pairs of properties simultaneously.
The researchers’ quantum-inspired analysis of neural network vulnerabilities suggests that adversarial attacks leverage the trade-off between the precision of input features and their computed gradients. “When considering the architecture of deep neural networks, which involve a loss function for learning, we can always define a conjugate variable for the inputs by determining the gradient of the loss function with respect to those inputs,” stated in the paper by Dr. Jun-Jie Zhang, whose expertise lies in mathematical physics.
This research is hopeful to prompt a reevaluation of the assumed robustness of neural networks and encourage a deeper comprehension of their limitations. By subjecting a neural network model to adversarial attacks, Dr. Zhang and Prof. Meng observed a compromise between the model’s accuracy and its resilience.
Interview with Gabriele Scheler: Neuro AI. Will it be the future?
Here is an interview concerning the current AI and generative AI waves, and their relation to neuroscience. We propose solutions based on new technology from neuroAI – which includes humans ability for reasoning, thought, logic, mathematics, proof etc. – and are therefore poorly modeled by data analysis on its own. Some of our work – also with scholars – has been published, while more is to come in a spin-off setting.
Josh Mitteldorf on programmed aging
Irina Conboy, Michael Conboy and Josh Mitteldorf discuss one of the central questions in aging research: is aging an active process of the body or is aging a passive process of damage accumulation? See the whole debate on our YouTube Channel: @HealesMovies Josh Mitteldorf, PhD, runs the blog “Aging Matters” (https://joshmitteldorf.scienceblog.com/) and is a consultant in mathematical modeling and creative data analysis. His research areas include evolutionary ecology, biology of aging, and the epidemiology of COVID-19. On the field of aging research, he has published two books,” Cracking The Aging Code”, co-written with Dorion Sagan (https://www.amazon.com/Cracking-Aging-Code-Science-Growing/d…atfound-20 and “Aging is a Group-Selected Adaptation” (https://drive.google.com/file/d/1bs0faQEV3T9cu-Eq079-e5bIGgMwNH08/view). Heales website (Healthy Life Extension Society): https://heales.org/ Subscribe to our newsletter: https://heales.org/newsletter/ Contact e-mail: [email protected] #science #aging #rejuvenation #biology #health #longevity #antiaging #debate #stemcells #programmedaging #entropy #cancer #conboy #conboys #mitteldorf Music: Closer To Your Dream by Keys of Moon | https://soundcloud.com/keysofmoon (CC BY 4.0)
Plunge into a Black Hole with NASA’s new immersive visualization (w/video)
Ever wonder what happens when you fall into a black hole? Now, thanks to a new, immersive visualization produced on a NASA supercomputer, viewers can plunge into the event horizon, a black hole’s point of no return.
In this visualization of a flight toward a supermassive black hole, labels highlight many of the fascinating features produced by the effects of general relativity along the way. Produced on a NASA supercomputer, the simulation tracks a camera as it approaches, briefly orbits, and then crosses the event horizon — the point of no return — of a monster black hole much like the one at the center of our galaxy. (Video: NASA’s Goddard Space Flight Center/J. Schnittman and B. Powell)
“People often ask about this, and simulating these difficult-to-imagine processes helps me connect the mathematics of relativity to actual consequences in the real universe,” said Jeremy Schnittman, an astrophysicist at NASA’s Goddard Space Flight Center in Greenbelt, Maryland, who created the visualizations. “So I simulated two different scenarios, one where a camera — a stand-in for a daring astronaut — just misses the event horizon and slingshots back out, and one where it crosses the boundary, sealing its fate.”

Visual Intuitive Physics: Enhancing Understanding Through Visualization
Often perceived as abstract and challenging, physics covers fundamental aspects of the universe, from the tiny world of quantum mechanics to the vast cosmos of general relativity. However, it often comes with intricate mathematical formulations that intimidate many learners. Visual Intuitive Physics is an emerging field that seeks to transform this complexity into accessible visual experiences, making physics more tangible and relatable. By employing visual aids and intuitive methodologies, this approach enhances the understanding of physical principles for students, researchers, and enthusiasts.
Understanding complex physics concepts often requires intuitive visualization that transcends verbal and mathematical explanations. Visualization in physics involves using graphs, diagrams, simulations, and other visual tools to provide a tangible understanding of abstract concepts. For instance, Marr and Bruce emphasized that visual tools significantly enhance conceptual understanding in students by providing concrete ways to comprehend physical laws.
Visualization helps bridge the gap between theoretical concepts and practical understanding. Per Kozma and Russell, visualization is pivotal in building cognitive structures that make understanding and remembering scientific principles easier. This is particularly significant for concepts that lack direct physical analogs, such as quantum mechanics and relativity.
New NASA Black Hole Visualization Takes Viewers Beyond the Brink
“People often ask about this, and simulating these difficult-to-imagine processes helps me connect the mathematics of relativity to actual consequences in the real universe,” said Jeremy Schnittman, an astrophysicist at NASA’s Goddard Space Flight Center in Greenbelt, Maryland, who created the visualizations. “So I simulated two different scenarios, one where a camera — a stand-in for a daring astronaut — just misses the event horizon and slingshots back out, and one where it crosses the boundary, sealing its fate.”
In the brain, bursts of beta rhythms implement cognitive control
Bursts of brain rhythms with “beta” frequencies control where and when neurons in the cortex process sensory information and plan responses. Studying these bursts would improve understanding of cognition and clinical disorders, researchers argue in a new review.
The brain processes information on many scales. Individual cells electrochemically transmit signals in circuits but at the large scale required to produce cognition, millions of cells act in concert, driven by rhythmic signals at varying frequencies. Studying one frequency range in particular, beta rhythms between about 14–30 Hz, holds the key to understanding how the brain controls cognitive processes — or loses control in some disorders — a team of neuroscientists argues in a new review article.
Drawing on experimental data, mathematical modeling and theory, the scientists make the case that bursts of beta rhythms control cognition in the brain by regulating where and when higher gamma frequency waves can coordinate neurons to incorporate new information from the senses or formulate plans of action. Beta bursts, they argue, quickly establish flexible but controlled patterns of neural activity for implementing intentional thought.
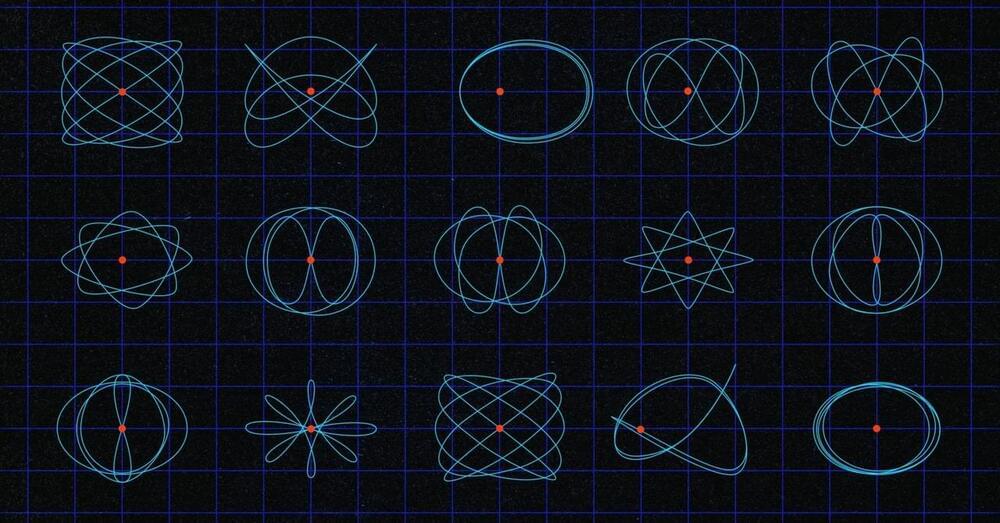
An Old Abstract Field of Math Is Unlocking the Deep Complexity of Spacecraft Orbits
The original version of this story appeared in Quanta Magazine.
In October, a Falcon Heavy rocket is scheduled to launch from Cape Canaveral in Florida, carrying NASA’s Europa Clipper mission. The $5 billion mission is designed to find out if Europa, Jupiter’s fourth-largest moon, can support life. But because Europa is constantly bombarded by intense radiation created by Jupiter’s magnetic field, the Clipper spacecraft can’t orbit the moon itself. Instead, it will slide into an eccentric orbit around Jupiter and gather data by repeatedly swinging by Europa—53 times in total—before retreating from the worst of the radiation. Every time the spacecraft rounds Jupiter, its path will be slightly different, ensuring that it can take pictures and gather data from Europa’s poles to its equator.
To plan convoluted tours like this one, trajectory planners use computer models that meticulously calculate the trajectory one step at a time. The planning takes hundreds of mission requirements into account, and it’s bolstered by decades of mathematical research into orbits and how to join them into complicated tours. Mathematicians are now developing tools which they hope can be used to create a more systematic understanding of how orbits relate to one another.

Physicists Say They May Have Found a Powerful Glitch in the Universe
Researchers have discovered what they’re calling a “cosmic glitch” in gravity, which could potentially help explain the universe’s strange behavior on a cosmic scale.
As detailed in a new paper published in the Journal of Cosmology and Astroparticle Physics, the team from the University of Waterloo and the University of British Columbia in Canada posit that Albert Einstein’s theory of general relativity may not be sufficient to explain the accelerating expansion of the universe.
Einstein’s “model of gravity has been essential for everything from theorizing the Big Bang to photographing black holes,” said lead author and Waterloo mathematical physics graduate Robin Wen in a statement about the research. “But when we try to understand gravity on a cosmic scale, at the scale of galaxy clusters and beyond, we encounter apparent inconsistencies with the predictions of general relativity.”