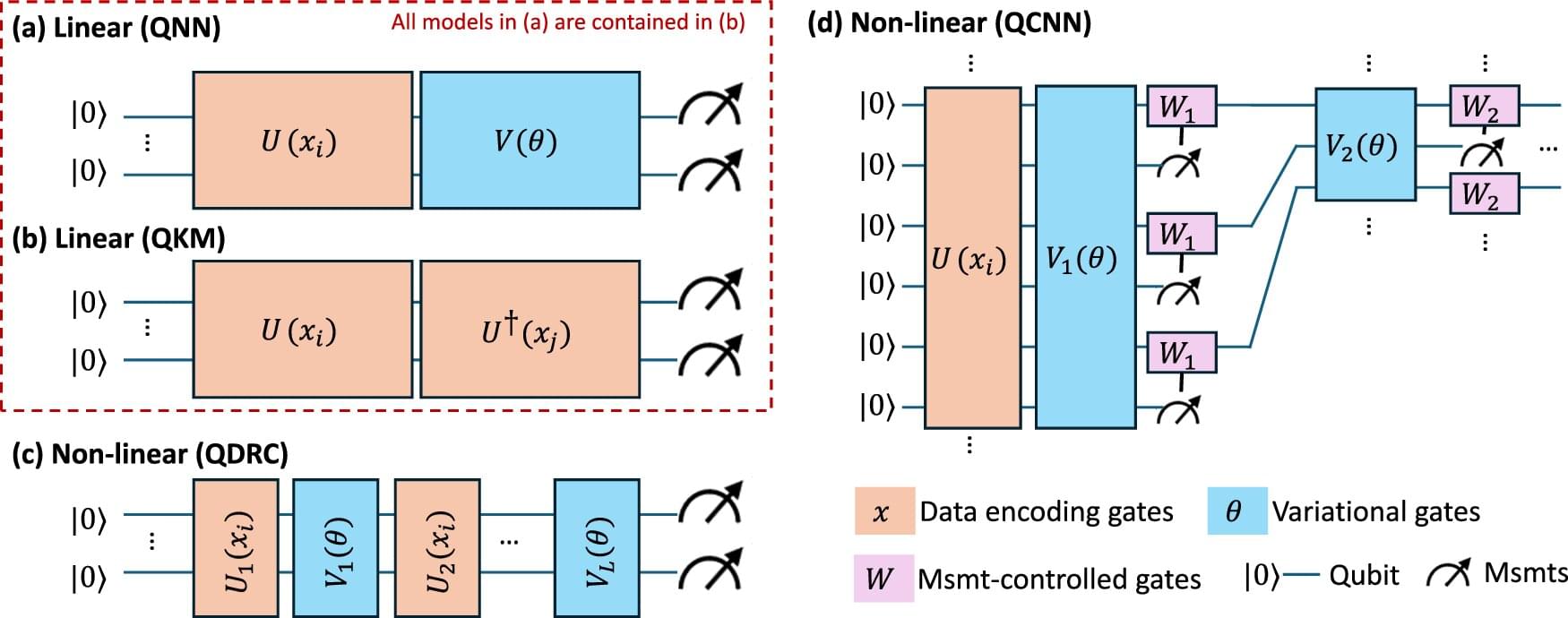
A broad systematic review has revealed that quantum computing applications in health care remain more theoretical than practical, despite growing excitement in the field.
The comprehensive study published in npj Digital Medicine, which analyzed 4,915 research papers published between 2015 and 2024, found little evidence that quantum machine learning (QML) algorithms currently offer any meaningful advantage over classical computing methods for health care applications.
“Despite exponential growth in research claiming quantum benefits for health care, our analysis shows no consistent evidence that quantum algorithms outperform classical methods for clinical decision-making or health service delivery,” said Dr. Riddhi Gupta from the School of Mathematics and Physics and the Queensland Digital Health Center (QDHeC) at the University of Queensland.