Musk said that the first human patient implanted with a Neuralink chip last month “is able to… move the mouse around the screen just by thinking.”


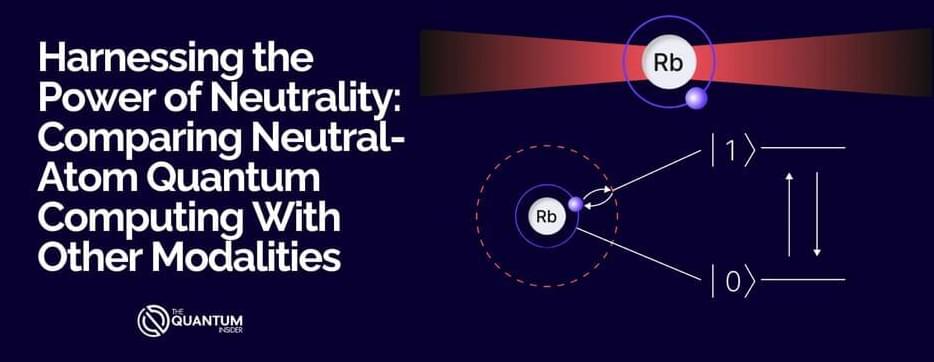
How Does The Neutral Atom Approach Compare
The neutral atom approach is a well-known and extensively investigated approach to quantum computing. The approach offers numerous advantages, especially in terms of scalability, expense, error mitigation, error correction, coherence, and simplicity.
Neutral atom quantum computing utilizes individual atoms, typically alkali atoms like rubidium or cesium, suspended and isolated in a vacuum and manipulated using precisely targeted laser beams. These atoms are not ionized, meaning they retain all their electrons and do not carry an electric charge, which distinguishes them from trapped ion approaches. The quantum states of these neutral atoms, such as their energy levels or the orientation of their spins, serve as the basis for qubits. By employing optical tweezers—focused laser beams that trap and hold the atoms in place—arrays of atoms can be arranged in customizable patterns, allowing for the encoding and manipulation of quantum information.

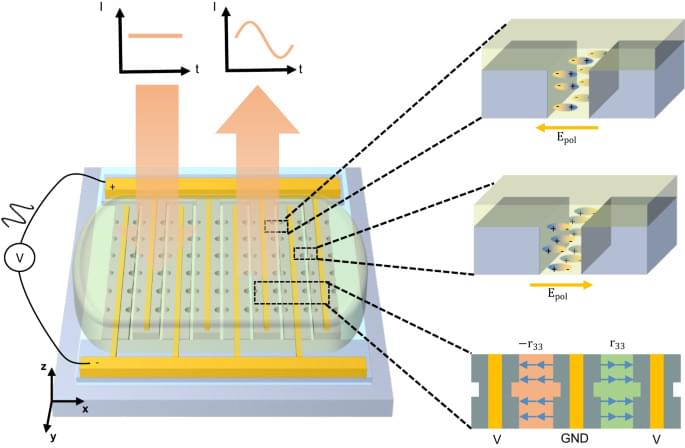
Relying on sub-wavelength nanostructures, metasurfaces have been shown as promising candidates for replacing conventional free-space optical components by arbitrarily manipulating the amplitude, phase, and polarization of optical wavefronts in certain applications1,2,3. In recent years, the scope of their applications has been expanded towards complete spatio-temporal control through the introduction of active metasurfaces. These developments open up exciting new possibilities for dynamic holography4, faster spatial light modulators5, and fast optical beam steering for LiDAR6. Large efforts have been channeled into various modulation mechanisms7. Microelectromechanical and nanoelectromechanical systems (MEMS and NEMS)8,9,10,11 have the advantages of low-cost and CMOS-compatibility, but the speed is limited up to MHz. Phase-change materials12,13,14 have fast, drastic, and non-volatile refractive index change, but lack continuous refractive index tuning and have a limited number of cycles constraining applicability to reconfigurable devices. Through molecule reorientation, liquid crystal can have index modulation over 10%, while under relatively low applied voltages Tunable liquid crystal metasurfaces, U.S. patent number 10,665,953 [Application Number 16/505,687]15. Techniques of liquid crystal integration have also advanced after decades of development. However, the tuning speeds are limited to kHz range16. Thermal-optic effects can induce relatively large refractive index changes17,18, but the speed is inherently limited and the on-chip thermal management can be challenging. The co-integration of transparent conductive oxide and metallic plasmonic structures5,6 has been demonstrated in epsilon-near-zero (ENZ) regime to control the wavefront of reflected light, but the low reflection amplitude induced by the optical loss of the materials and the ENZ regime is unavoidable.
In modern photonics, a multitude of technologies for tunable optics and frequency conversion19,20 are realized with nonlinear materials that have low loss and a strong χ effect, such as lithium niobate21,22, aluminum nitride23, and organic electro-optic (OEO) materials24. Their ultrafast responses make it possible to use RF or millimeter-wave control25. Developments in computational chemistry have also led to artificially engineered organic molecules that have record-high nonlinear coefficients with long-term and high-temperature stability26,27. However, their potential in modifying free-space light has been relatively unexplored until recently. Several OEO material-hybrid designs have demonstrated improved tunability of metasurfaces28,29,30. Utilizing dielectric resonant structures and RF-compatible coplanar waveguides, a free-space silicon-organic modulator has recently accomplished GHz modulation speed31. However, all demonstrations to date require high operating voltages ± 60V, due to low resonance tuning capability (frequency shift / voltage), which hinders their integration with electronic chips.
In this work, we propose combining high-Q metasurfaces based on slot-mode resonances with the unique nano-fabrication techniques enabled by OEO materials, which drastically reduces the operating voltage. The low voltage is mainly achieved from the ability to place the electrodes in close proximity to each other while hosting high-Q modes in between and the large overlap of the optical and RF fields in OEO materials. In the following sections, we first provide the design concepts and considerations for achieving a reduced operating voltage. Next, we numerically demonstrate the advantage of a particular selected mode compared to other supported modes in the structure. Finally, we experimentally realize our concepts and characterize the performance of the electro-optic metasurface.
MIT researchers used ultrathin van der Waals materials to create an electron magnet that can be switched at room temperature. This type of magnet could be used to build magnetic processors or memories that would consume far less energy than silicon devices.

Neuralink’s first human patient able to use mouse…:
Elon Musk is the visionary behind Neuralink. He announced that the first human recipient of the company’s brain chip implant has fully recovered. The individual has demonstrated the ability to use a computer mouse solely through thoughts. Watch this video for all details.
#Neuralink #ElonMusk #WION
About Channel:
WION The World is One News examines global issues with in-depth analysis. We provide much more than the news of the day. Our aim is to empower people to explore their world. With our Global headquarters in New Delhi, we bring you news on the hour, by the hour. We deliver information that is not biased. We are journalists who are neutral to the core and non-partisan when it comes to world politics. People are tired of biased reportage and we stand for a globalized united world. So for us, the World is truly One.

Creating a quantum computer powerful enough to tackle problems we cannot solve with current computers remains a big challenge for quantum physicists. A well-functioning quantum simulator – a specific type of quantum computer – could lead to new discoveries about how the world works at the smallest scales. Quantum scientist Natalia Chepiga from Delft University of Technology has developed a guide on how to upgrade these machines so that they can simulate even more complex quantum systems. The study is now published in Physical Review Letters.
“Creating useful quantum computers and quantum simulators is one of the most important and debated topics in quantum science today, with the potential to revolutionize society,” says researcher Natalia Chepiga. Quantum simulators are a type of quantum computer, Chepiga explains: “Quantum simulators are meant to address open problems of quantum physics to further push our understanding of nature. Quantum computers will have wide applications in various areas of social life, for example in finances, encryption, and data storage.”
Steering Wheel

“The fact that the groundwater isn’t as big of a process could mean that other things are,” said Eric Hiatt. “It might magnify the importance of runoff, or it could mean that it just didn’t rain as much on Mars. But it’s just fundamentally different from how we think about [water] on Earth.”
How much water on ancient Mars fell into aquifers to refill groundwater? This is what a recent study published in Icarus hopes to address as a team of international researchers led by The University of Texas at Austin (UTA) used computer models to calculate groundwater recharge rates in the southern highlands of ancient Mars. This study holds the potential to help scientists better understand the amount of water that potentially existed on ancient Mars and what this could mean for finding ancient life on the Red Planet.
For the study, the researchers used a combination of previously used and new computer modeling techniques to estimate how much groundwater recharge occurred in the Martian southern highlands, since most of the liquid water that existed on Mars billions of years ago resided in a vast ocean in the northern lowlands. In the end, the researchers found the aquifers in the southern highlands on Mars experienced an average groundwater recharge of only 0.03 millimeters (0.001 inches) per year. For context, the Trinity and Edwards-Trinity Plateau aquifers that are responsible for providing water for the city of San Antonio range between 2.5 to 50 millimeters (0.1 inches to 2 inches) per year, or between 80 and 1,600 times that of the Martian aquifers.

Forward-looking: As consumers increasingly turn toward digital distribution and data center operators try various storage methods, optical discs haven’t stopped evolving. A recently published paper explains how manufacturers could make DVD-like discs that hold the equivalent of hundreds or thousands of Blu-rays.
Researchers at the University of Shanghai for Science and Technology have developed an optical disc with a capacity of over a petabit of data, equivalent to well over 100 terabytes. Although the technology is primarily proposed for enterprise use, it could potentially become accessible to consumers after overcoming significant obstacles.
The scientists were able to significantly increase the capacity of an optical disc by implementing a 3D planar recording architecture. The technology uses a highly transparent, uniform photoresist film doped with aggregation-induced emission dye and stimulated by femtosecond lasers.