Eating a type of dietary fiber called chitin evoked an immune response in mice that was linked to better metabolic health.



MDPI uses a print-on-demand service. Your book will be printed and delivered directly from one of three print stations, allowing you to profit from economic shipping to any country in the world. Generally, we use Premium shipping with an estimated delivery time of 7–12 business days. P.O. Boxes cannot be used as a Ship-To Address.
Please note that shipping time does not include the time for placing and processing the order or printing. For this, an additional turnaround time of 10 working days should be expected.
Neurosurgeons can leave the operating room more confident today than ever before about their patient’s brain tumor diagnosis, thanks to the integration of a new system that employs optical imaging and artificial intelligence that are making brain tumor diagnosis quicker and more accurate. This technology is allowing them to quickly see diagnostic tissue and tumor margins in near-real time.
For the full story, visit: http://michmed.org/gk8ZD
Learn more about the scientific breakthroughs happening at Michigan Medicine, visit: https://labblog.uofmhealth.org/
Follow Michigan Medicine on Social:
Twitter: https://twitter.com/umichmedicine.
Instagram: https://www.instagram.com/umichmedicine/
Facebook: https://www.facebook.com/MichiganMedicine/
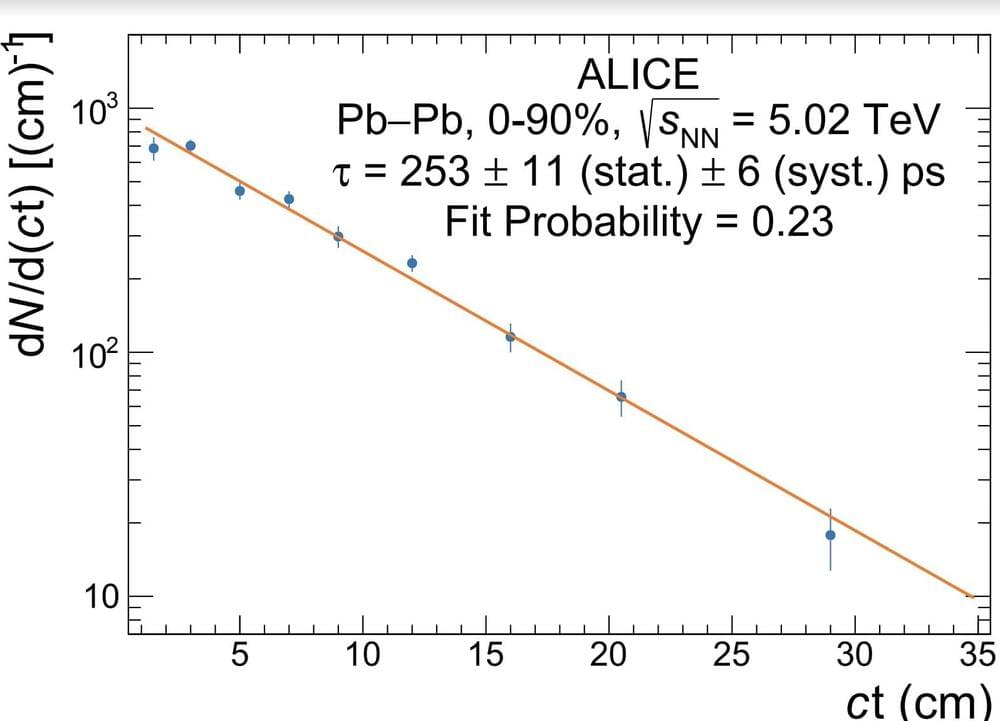
A hypertriton is a tritium nucleus in which a neutron is replaced by a so-called Lambda hyperon. This type of hypernucleus was first discovered in the 1950s has since been the key focus of numerous studies.
The ALICE collaboration, a large research group that studies the collisions of nuclei inside CERN’s large hadron collider (LHC) in Switzerland, recently measured the lifetime of a hypertriton with remarkable precision. Their paper, published in Physical Review Letters, is a further step forward toward understanding the unique properties of these fascinating nuclear complexes.
“As the first and lightest hypernucleus (i.e., a nucleus that includes a baryon with at least one strange quark) ever identified, the hypertriton holds a special place in nuclear physics,” Maximiliano Puccio, part of the ALICE collaboration, told Phys.org.
An international research team has taken a decisive step toward a new generation of atomic clocks. At the European XFEL X-ray laser, the researchers have created a much more precise pulse generator based on the element scandium, which enables an accuracy of one second in 300 billion years—that is about a thousand times more precise than the current standard atomic clock based on cesium. The team presents its success in the journal Nature.
Atomic clocks are currently the world’s most accurate timekeepers. These clocks have used electrons in the atomic shell of chemical elements, such as cesium, as a pulse generator in order to define the time. These electrons can be raised to a higher energy level with microwaves of a known frequency. In the process, they absorb the microwave radiation.
An atomic clock shines microwaves at cesium atoms and regulates the frequency of the radiation such that the absorption of the microwaves is maximized; experts call this a resonance. The quartz oscillator that generates the microwaves can be kept so stable with the help of resonance that cesium clocks will be accurate to within one second within 300 million years.
For those still holding out hope that antimatter levitates rather than falls in a gravitational field, like normal matter, the results of a new experiment are a dose of cold reality.
Physicists studying antihydrogen—an anti-proton paired with an antielectron, or positron—have conclusively shown that gravity pulls it downward and does not push it upward.
At least for antimatter, antigravity doesn’t exist.
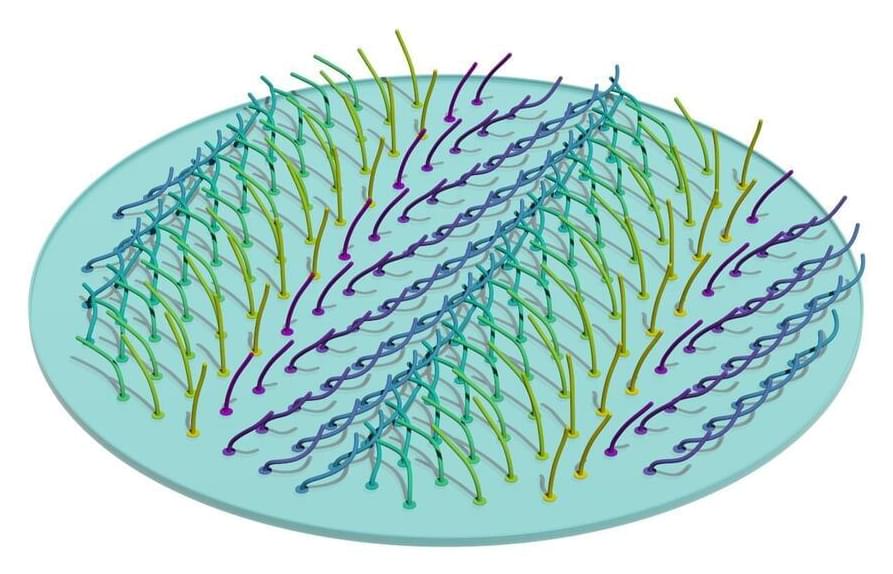
What do the crowd at a football stadium, the feet of a centipede, and the inside of your lungs have in common? All of these systems show the same specific kind of organization, as recently discovered by a group of scientists from MPI-DS.
The crowd wave in a stadium looks like a pattern traveling across the tiers. Similarly, the legs of a centipede move in canon with illusory waves sweeping along its entire length. On a microscopic level, tiny hairs in our lungs called cilia wave together to transport mucus. This serves as a first line of defense against invading pathogens.
To create a synchronized and efficient wave, cilia need to accurately coordinate their beating motion. Unlike football fans watching their neighbors and the nervous system coordinating the centipede’s legs, cilia have no such intelligent control system.

Every so often, astronomers glimpse an intense flash of radio waves from space—a flash that lasts only instants but puts out as much energy in a millisecond as the sun does in a few years. The origin of these “fast radio bursts” is one of the greatest mysteries in astronomy today.
There is no shortage of ideas to explain the cause of the bursts: a catalog of current theories shows more than 50 potential scenarios. You can take your pick from highly magnetized neutron stars, collisions of incredibly dense stars or many more extreme or exotic phenomena.
How can we figure out which theory is correct? One way is to look for more information about the bursts, using other channels: specifically, using ripples in the fabric of the universe called gravitational waves.
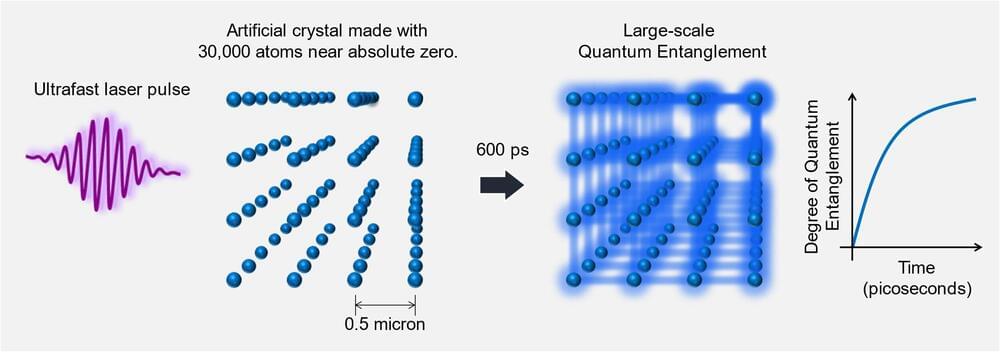
A research group led by Professor Kenji Ohmori at the Institute for Molecular Science, National Institutes of Natural Sciences are using an artificial crystal of 30,000 atoms aligned in a cubic array with a spacing of 0.5 micron, cooled to near absolute zero temperature. By manipulating the atoms with a special laser light that blinks for 10 picoseconds, they succeeded in executing quantum simulation of a model of magnetic materials.
Their novel “ultrafast quantum computer” scheme demonstrated last year was applied to quantum simulation. Their achievement shows that their novel “ultrafast quantum simulator” is an epoch-making platform, as it can avoid the issue of external noise, one of the biggest concerns for quantum simulators. The “ultrafast quantum simulator” is expected to contribute to the design of functional materials and the resolution of social problems.
Their results were published online in Physical Review Letters.