Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog – Page 3

Get the latest international news and world events from around the world.

Log in for authorized contributors

Nanoparticle therapy reprograms tumor immune cells to attack cancer from within

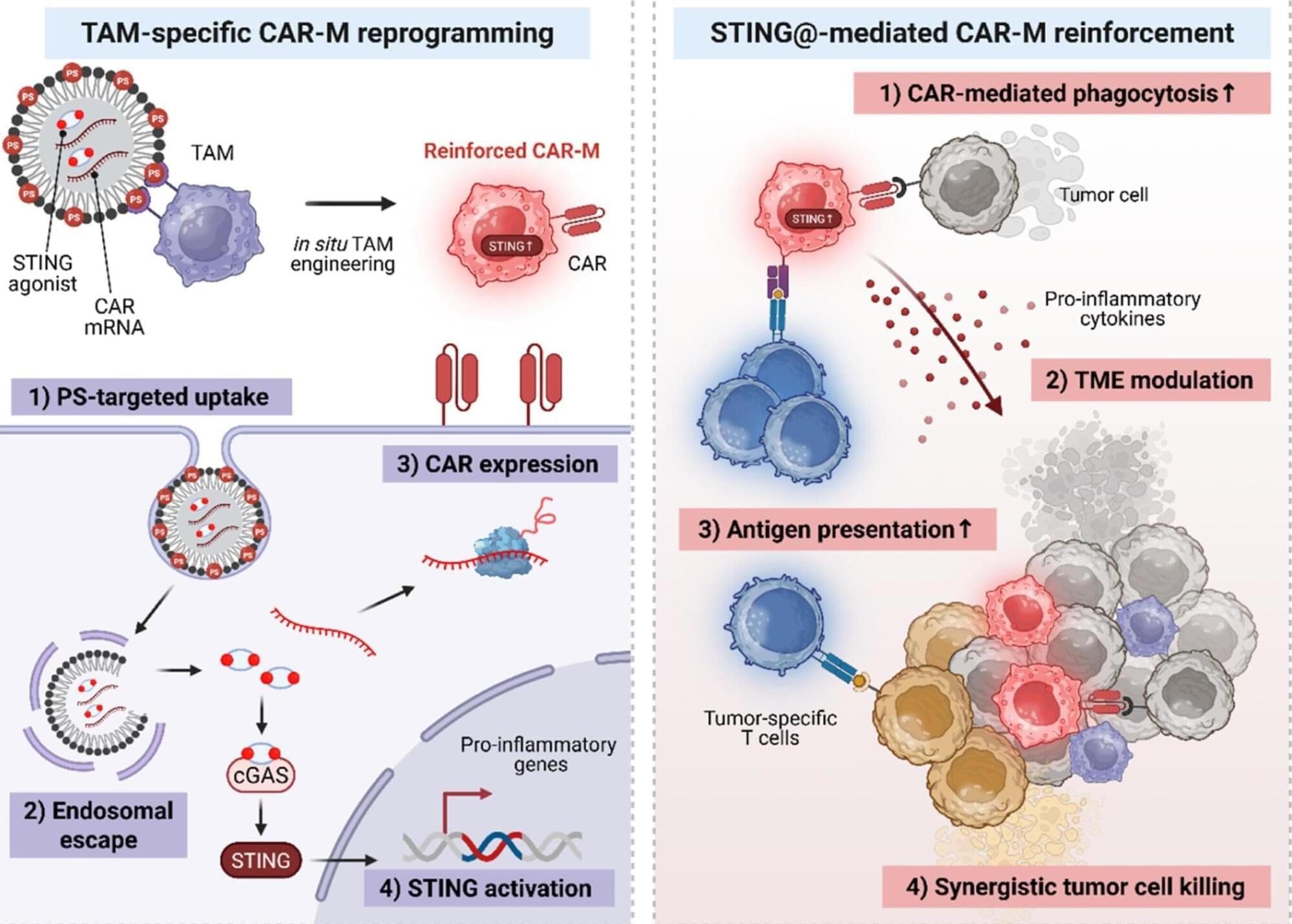
Within tumors in the human body, there are immune cells (macrophages) capable of fighting cancer, but they have been unable to perform their roles properly due to suppression by the tumor. A KAIST research team led by Professor Ji-Ho Park of the Department of Bio and Brain Engineering have overcome this limitation by developing a new therapeutic approach that directly converts immune cells inside tumors into anticancer cell therapies.

In their approach, when a drug is injected directly into a tumor, macrophages already present in the body absorb it, produce CAR (a cancer-recognizing device) proteins on their own, and are converted into anticancer immune cells known as “CAR-macrophages.” The paper is published in the journal ACS Nano.

Solid tumors —such as gastric, lung, and liver cancers—grow as dense masses, making it difficult for immune cells to infiltrate tumors or maintain their function. As a result, the effectiveness of existing immune cell therapies has been limited.

Melanoma cancer cells secrete extracellular vesicles to paralyze immune cells

A new international study led by Prof. Carmit Levy of the Department of Human Genetics and Biochemistry at the Gray Faculty of Medical & Health Sciences at Tel Aviv University finds that melanoma cancer cells paralyze immune cells by secreting extracellular vesicles (EVs), which are tiny, bubble-shaped containers secreted from a given cell. The research team believes that this discovery has far-reaching implications for possible treatments for the deadliest form of skin cancer.

The work is published in the journal Cell.

Melanoma is the deadliest type of skin tumor. In the first stage of the disease, melanocytic cells divide uncontrollably in the skin’s outer layer, the epidermis. In the second stage, the cancer cells invade the inner dermis layer and metastasize through the lymphatic and blood systems.

Currents 072: Ben Goertzel on Viable Paths to True AGI

https://www.jimruttshow.com/currents-ben-goertzel-2/

Jim talks with Ben Goertzel about the ideas in his recent essay “Three Viable Paths to True AGI.” They discuss the meaning of artificial general intelligence, Steve Wozniak’s basic AGI test, whether common tasks actually require AGI, a conversation with Joscha Bach, why deep neural nets are unsuited for human-level AGI, the challenge of extrapolating world-models, why imaginative improvisation might not be interesting to corporations, the 3 approaches that might have merit (cognition-level, brain-level, and chemistry-level), the OpenCog system Ben is working on, whether it’s a case of “good old-fashioned AI,” where evolution fits into the approach, why deep neural nets aren’t brain simulations & attempts to make them more realistic, a hypothesis about how to improve generalization, neural nets for music & the psychological landscape of AGI research, algorithmic chemistry & the origins of life problem, why AGI deserves more resources than it’s getting, why we may need better parallel architectures, how & how much society should invest in new approaches, the possibility of a cultural shift toward AGI viability, and much more.

Tokamak experiments exceed plasma density limit, offering new approach to fusion ignition

Researchers working on China’s fully superconducting Experimental Advanced Superconducting Tokamak (EAST) have experimentally accessed a theorized “density-free regime” for fusion plasmas, achieving stable operation at densities well beyond conventional limits.

The results, reported in Science Advances, provide new insights into overcoming one of the most persistent physical obstacles on the path toward nuclear fusion ignition.

The study was co-led by Prof. Zhu Ping from Huazhong University of Science and Technology and Associate Prof. Yan Ning from the Hefei Institutes of Physical Science of the Chinese Academy of Sciences. By realizing a novel high-density operating scheme on EAST, the team demonstrated that plasma density, long constrained by empirical limits in tokamak operation, can be substantially extended without triggering disruptive instabilities.

Forget Transistors: This New “Intelligent” Material Computes Like a Human Brain

Tiny molecules that can think, remember, and learn may be the missing link between electronics and the brain. For more than half a century, researchers have looked for ways to move past silicon by building electronics from molecules. The idea sounded simple and beautiful, but real devices turned

Neuralink plans ‘high-volume’ brain implant production by 2026, Musk says

Elon Musk’s brain implant company Neuralink will start “high-volume production” of brain-computer interface devices and move to an entirely automated surgical procedure in 2026, Musk said in a post on the social media platform X on Wednesday.

The origin of space time matter and everything

On the Same Origin of Spacetime, Matter, and Everything https://lnkd.in/gCs9XBzx What if space, time, matter, gravity, dark matter, and dark energy all come from one thing: quantum entanglement? 1. Reality starts as a quantum state (not spacetime) In EWOG, the universe does **not** begin with space and time. It begins with a single quantum state: |Ψ⟩ ∈ No coordinates No distances No clocks Only quantum information. ➡ Spacetime appears later. 2. Geometry is quantum, not classical Spacetime is not a background — it is made of operators: ĝ_μν, R̂_μν, R̂ What we experience as classical spacetime is just the **average**: g_μν = ⟨ ĝ_μν ⟩ Intuition: Spacetime is a *shadow* cast by quantum entanglement. 3.

/* */