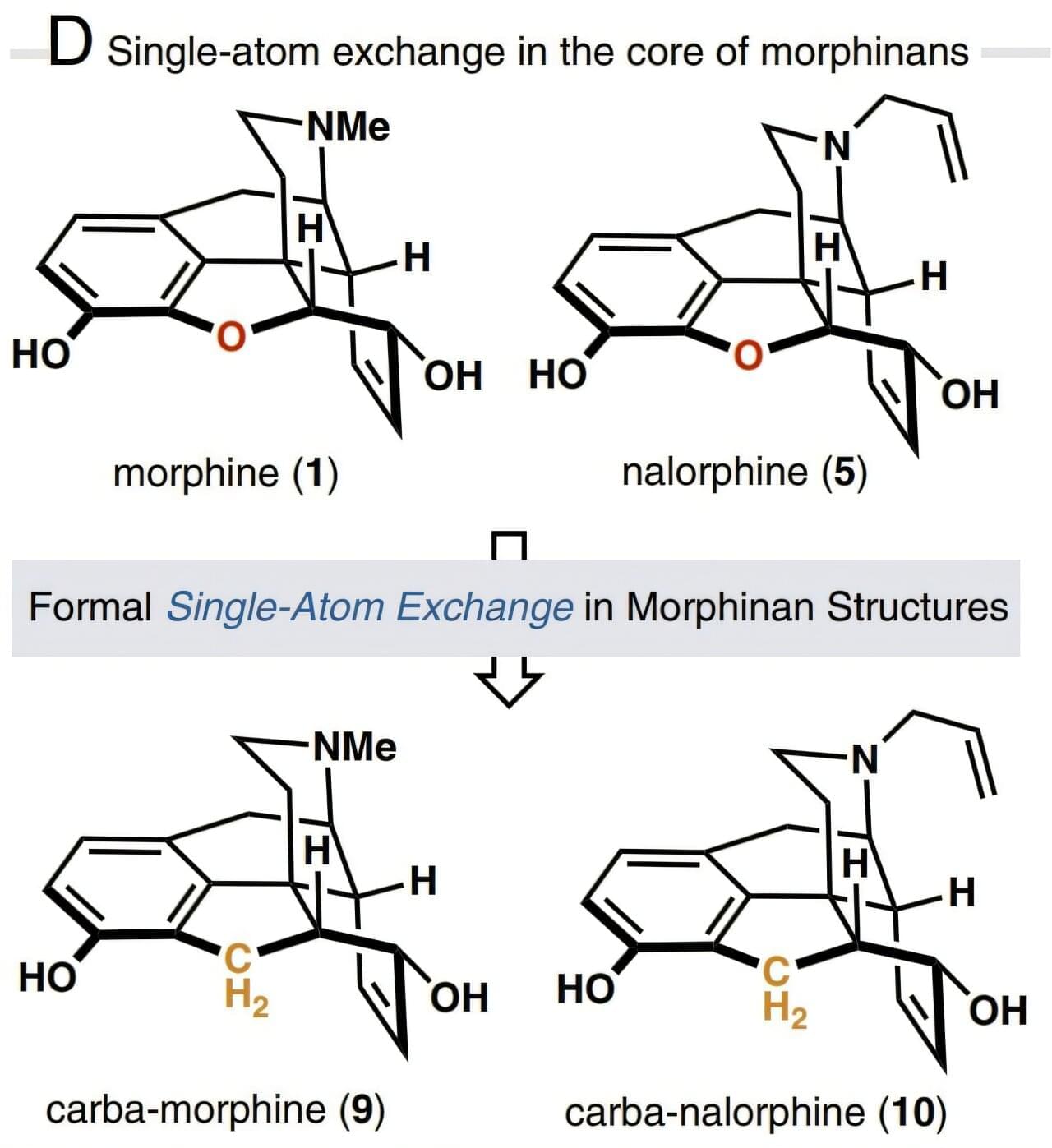
One of the greatest revolutions in the field of pain medication was the isolation of morphine from the opium poppy in the 19th century. Morphine molecules act as painkillers by attaching themselves to the µ-opioid receptor (MOR) in the central nervous system and blocking the brain from sending pain signals to the rest of the body. This potent opioid analgesic also has side effects such as constipation, respiratory depression, and even serious addiction problems.
A new study published in the Proceedings of the National Academy of Sciences has found that a single heavy atom replacement in the morphine core structure can transform its pharmacological behavior, resulting in reduced respiratory depression and no evidence of reward behavior—a key component of addiction tendencies—even at high doses.
Based on the insight that core-atom changes to the opioid drug molecule may exhibit biological effects distinct from the parent compound, the researchers developed a 15-step total synthesis of a morphine derivative where an oxygen atom in the E-ring is replaced with a methylene (CH2) group and called the new derivative carbamorphine.