Nonlinear optics explores how powerful light (e.g. lasers) interacts with materials, resulting in the output light changing colour (i.e. frequency) or behaving differently based on the intensity of the incoming light. This field is crucial for developing advanced technologies such as high-speed communication systems and laser-based applications. Nonlinear optical phenomena enable the manipulation of light in novel ways, leading to breakthroughs in fields like telecommunications, medical imaging, and quantum computing. Two-dimensional (2D) materials, such as graphene—a single layer of carbon atoms in a hexagonal lattice—exhibit unique properties due to their thinness and high surface area. Graphene’s exceptional electronic properties, related to relativistic-like Dirac electrons and strong light-matter interactions, make it promising for nonlinear optical applications, including ultrafast photonics, optical modulators, saturable absorbers in ultrafast lasers, and quantum optics.
Dr. Habib Rostami, from the Department of Physics at the University of Bath, has co-authored pioneering research published in Advanced Science. This study involved an international collaboration between an experimental team at Friedrich Schiller University Jena in Germany and theoretical teams at the University of Pisa in Italy and the University of Bath in the UK. The research aimed to investigate the ultrafast opto-electronic and thermal tuning of nonlinear optics in graphene.
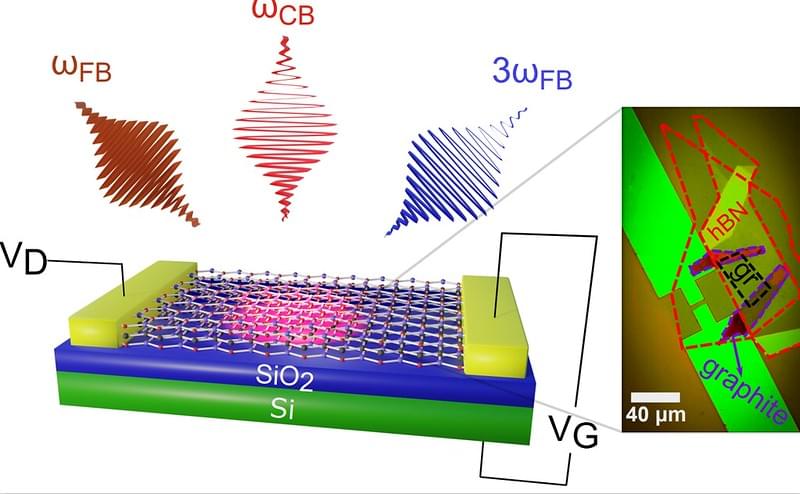
This study discovers a new way to control high-harmonic generation in a graphene-based field-effect transistor. The team investigated the impact of lattice temperature, electron doping, and all-optical ultrafast tuning of third-harmonic generation in a hexagonal boron nitride-encapsulated graphene opto-electronic device. They demonstrated up to 85% modulation depth along with gate-tuneable ultrafast dynamics, a significant improvement over previous static tuning. Furthermore, by changing the lattice temperature of graphene, the team could enhance the modulation of its optical response, achieving a modulation factor of up to 300%. The experimental fabrication and measurement took place at Friedrich Schiller University Jena. Dr. Rostami played a crucial role in the study by crafting theoretical models. These models were developed in collaboration with another theory team at the University of Pisa to elucidate new effects observed in graphene.