A new study in Physical Review Letters has used atomic clocks to study relativistic effects in interacting quantum systems.


Scientists have developed a quantum computer that uses light to process data, paving the way for quantum computers that can operate in a networked environment at room temperature.
The new system, called Aurora, is the first photonic quantum computer in the world that can operate at scale using several modules interconnected through fiber optic cables. The system presents a solution to some of quantum computing’s biggest problems — namely operation at scale, fault tolerance and error correction, Xanadu representatives say.

The speed of light is often regarded as the ultimate cosmic speed limit, but researchers have now managed to slow it down dramatically—to just 61 kilometers per hour. This was achieved by using a Bose-Einstein condensate (BEC), a peculiar quantum state of matter that allows light to be slowed or even stopped entirely. This discovery, which builds on decades of research, has implications for quantum physics, computing, and information storage.
The Quantum Jelly Effect In everyday conditions, light moves at 299,792,458 meters per second in a vacuum, and its speed decreases slightly when passing through materials like glass or water. However, these reductions are relatively small. In contrast, when light travels through a Bose-Einstein condensate, it can be slowed to a near standstill.
A Bose-Einstein condensate is an exotic state of matter, first predicted by Albert Einstein and Satyendra Nath Bose, that occurs when a gas is cooled to temperatures just above absolute zero. Under these conditions, the atoms behave as a single quantum entity, exhibiting superfluidity and interacting with light in ways not seen in ordinary materials.

For over a century, physicists have grappled with one of the most profound questions in science: How do the rules of quantum mechanics, which govern the smallest particles, fit with the laws of general relativity, which describe the universe on the largest scales?
The optical lattice clock, one of the most precise timekeeping devices, is becoming a powerful tool used to tackle this great challenge. Within an optical lattice clock, atoms are trapped in a “lattice” potential formed by laser beams and are manipulated with precise control of quantum coherence and interactions governed by quantum mechanics.
Simultaneously, according to Einstein’s laws of general relativity, time moves slower in stronger gravitational fields. This effect, known as gravitational redshift, leads to a tiny shift of atoms’ internal energy levels depending on their position in gravitational fields, causing their “ticking”—the oscillations that define time in optical lattice clocks—to change.

Many physicists and engineers have recently been trying to demonstrate the potential of quantum computers for tackling some problems that are particularly demanding and are difficult to solve for classical computers. A task that has been found to be challenging for both quantum and classical computers is finding the ground state (i.e., lowest possible energy state) of systems with multiple interacting quantum particles, called quantum many-body systems.
When one of these systems is placed in a thermal bath (i.e., an environment with a fixed temperature that interacts with the systems), it is known to cool down without always reaching its ground state. In some instances, a quantum system can get trapped at a so-called local minimum; a state in which its energy is lower than other neighboring states but not at the lowest possible level.
Researchers at California Institute of Technology and the AWS Center for Quantum Computing recently showed that while finding the local minimum for a system is difficult for classical computers, it could be far easier for quantum computers.

A small international team of nanotechnologists, engineers and physicists has developed a way to force laser light into becoming a supersolid. Their paper is published in the journal Nature. The editors at Nature have published a Research Briefing in the same issue summarizing the work.
Supersolids are entities that exist only in the quantum world, and, up until now, they have all been made using atoms. Prior research has shown that they have zero viscosity and are formed in crystal-like structures similar to the way atoms are arranged in salt crystals.
Because of their nature, supersolids have been created in extremely cold environments where the quantum effects can be seen. Notably, one of the team members on this new effort was part of the team that demonstrated more than a decade ago that light could become a fluid under the right set of circumstances.
“Nanobrain: The Making of an Artificial Brain from a Time Crystal” by Anirban Bandyopadhyay Book Link: https://amzn.to/3QQ4s44
The hosts discuss the book “Nanobrain” by Anirban Bandyopadhyay, an in-depth exploration of a nanobrain, an artificial brain built on the principles of fractal geometry and prime numbers, which claims to mimic human thought. It introduces Prime Phase Metric (PPM) which expands time crystals from natural events, and Geometric Musical Language (GML) which assigns fifteen primes to letters, similar to the English alphabet, and how the combination is consciousness-centric. The document contrasts this artificial brain’s functioning with traditional Turing machines and quantum computing, emphasizing its unique approach to data processing and decision-making and self-learning, and discusses its potential limitations and advantages. It investigates the use of time crystals, dynamic geometric shapes, and fractal mechanics, and the role that they may have in memory and learning in this new computer. Finally, the work explores the philosophical implications of such a machine, including its potential for achieving consciousness and the idea of recreating nature through a non-computational paradigm, such as modeling a new type of robot.
#ArtificialIntelligence #AIRevolution #Nanobrain #TimeCrystals #QuantumAI #FutureofAI #AIBreakthrough #NextGenAI #TechTrends #AIHardware #NaturalAI #NoCodeAI #SelfLearningAI #AIAAlternative #BrainAI #NewMachine #FutureMachine #AdvancedAI #InformationReality #PhysicsMetaphysics #NatureOfReality #QuantumInformation #BiologicalInformation #PhilosophyOfScience #ScienceAndTheology #CosmicInformation #OriginOfLife #UltimateReality #MeaningOfInformation #ComplexSystems #HistoryOfScience #Interdisciplinary #SciencePhilosophy #deepdive #skeptic #podcast #synopsis #books #bookreview #ai #artificialintelligence #booktube #aigenerated #history #alternativehistory #aideepdive #ancientmysteries #hiddenhistory #futurism #videoessay #primenumber

A new understanding of how an observer can change the disorder, or entropy, of a quantum object could help us probe how gravity interacts with the quantum realm.
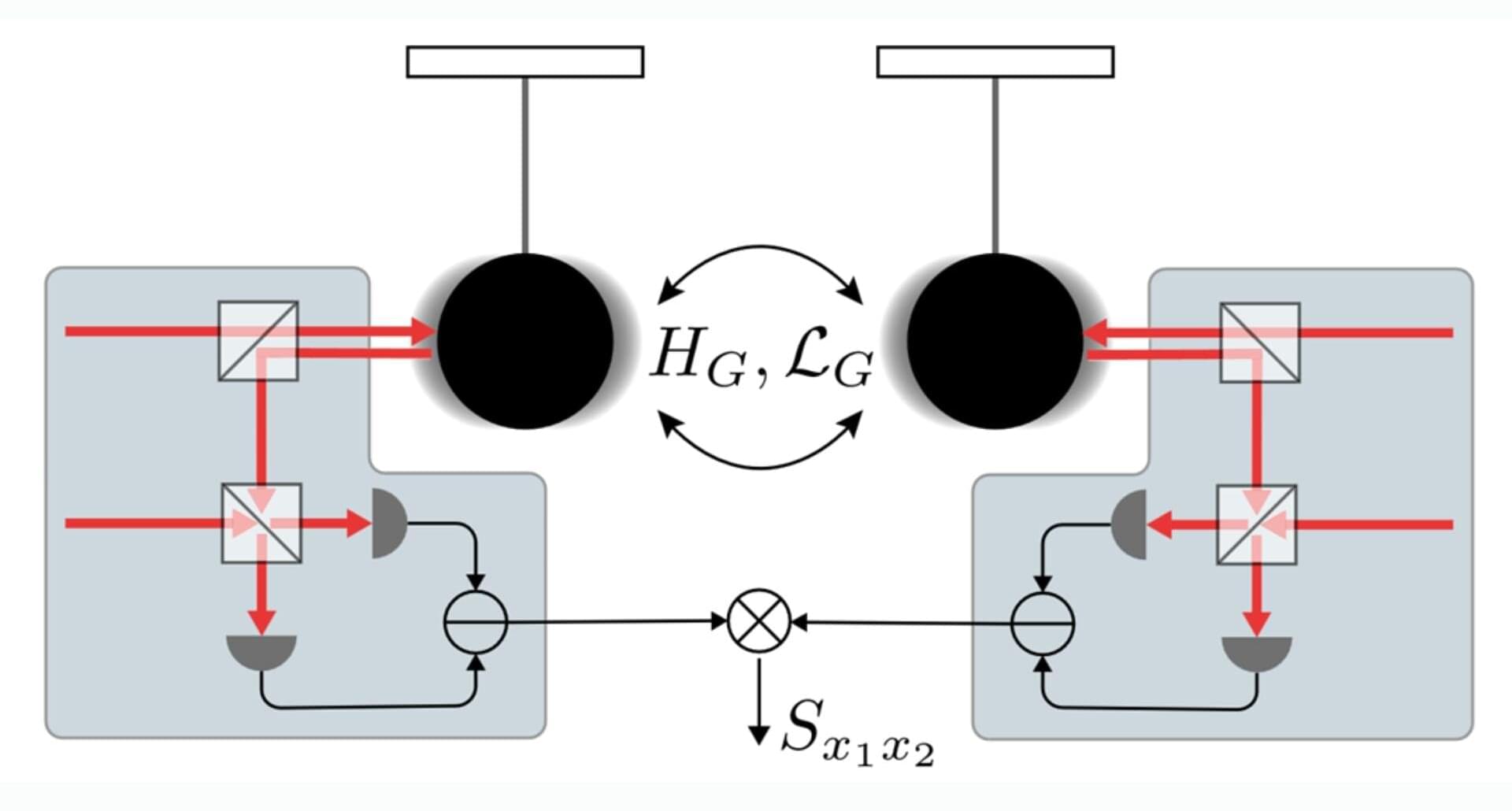
In a new Physical Review Letters study, researchers propose an experimental approach that could finally determine whether gravity is fundamentally classical or quantum in nature.
The nature of gravity has puzzled physicists for decades. Gravity is one of the four fundamental forces, but it has resisted integration into the quantum framework, unlike the electromagnetic, strong, and weak nuclear forces.
Rather than directly tackling the challenging problem of constructing a complete quantum theory of gravity or trying to detect individual gravitons—the hypothetical mediator of gravity—the researchers take a different approach.
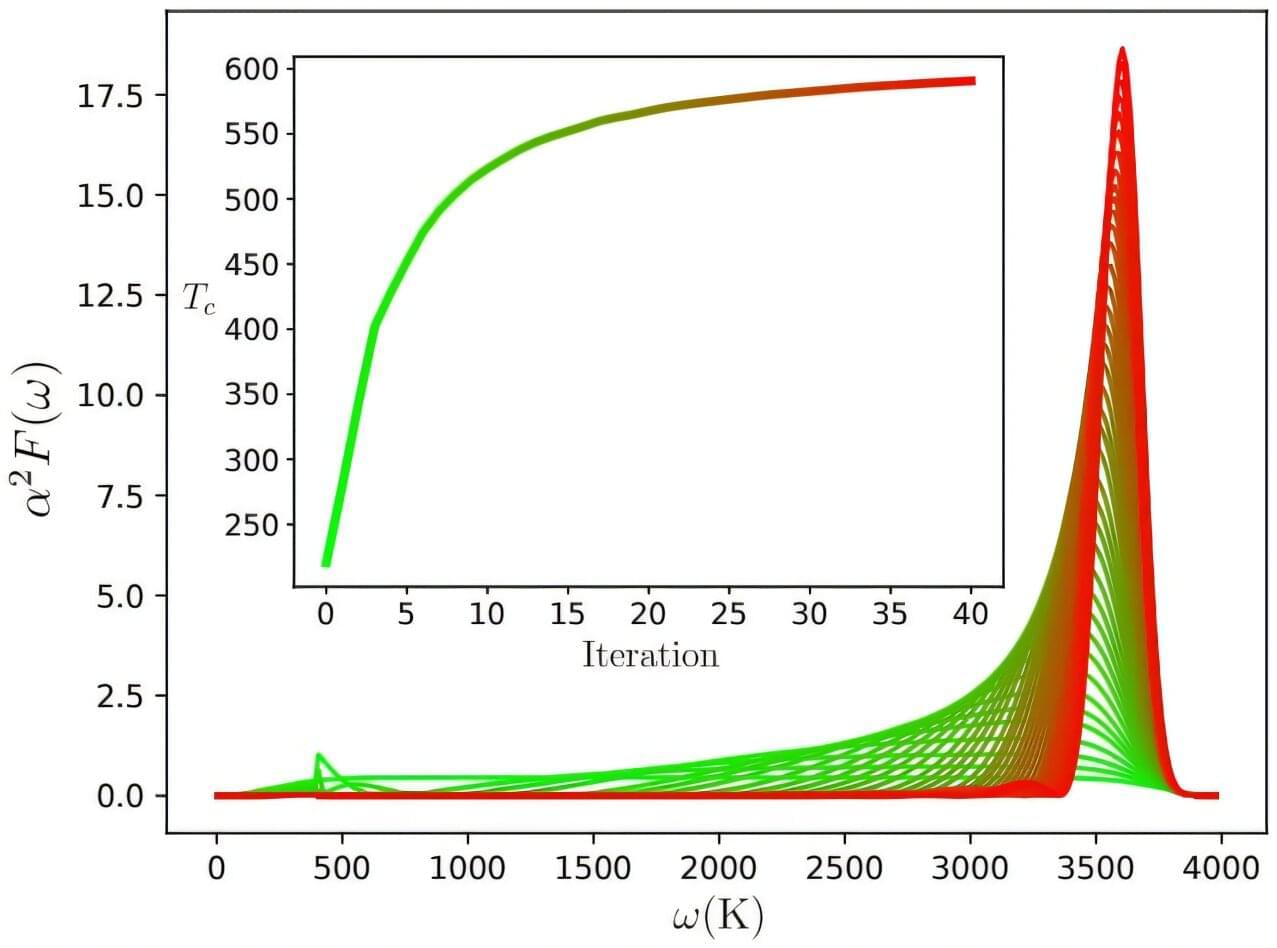
In a new development that could help redefine the future of technology, a team of physicists has uncovered a fundamental insight into the upper limit of superconducting temperature.
This research, accepted for publication in the Journal of Physics: Condensed Matter, suggests that room-temperature superconductivity —long considered the “holy grail” of condensed matter physics—may indeed be possible within the laws of our universe.
Superconductors, materials that can conduct electricity without resistance, have the potential to revolutionize energy transmission, medical imaging, and quantum computing. However, until now, they have only functioned at extremely low temperatures, making them impractical for widespread use. The race to find a superconductor that works at ambient conditions has been one of the most intense and elusive pursuits in modern science.