Finding new materials with useful properties is a primary goal for materials scientists, and it’s central to improving technology. One exciting area of current research is 2D materials—super-thin substances made of just a few layers of atoms, which could power the next generation of electronic devices. In a new study, researchers at the University of Maryland Baltimore County (UMBC) developed a new way to predict 2D materials that might transform electronics. The results were published in Chemistry of Materials on July 7.
Picture a sheet of paper so thin that it’s only a few atoms thick, and that’s what 2D materials are like. One might think they would be fragile—but these materials can actually be incredibly strong or conduct electricity in unique ways. They’re held together by weak forces called van der Waals bonds, which allow materials to slightly deform without breaking under stress. Stacked layers of these 2D materials can slide past each other, further reducing brittleness.
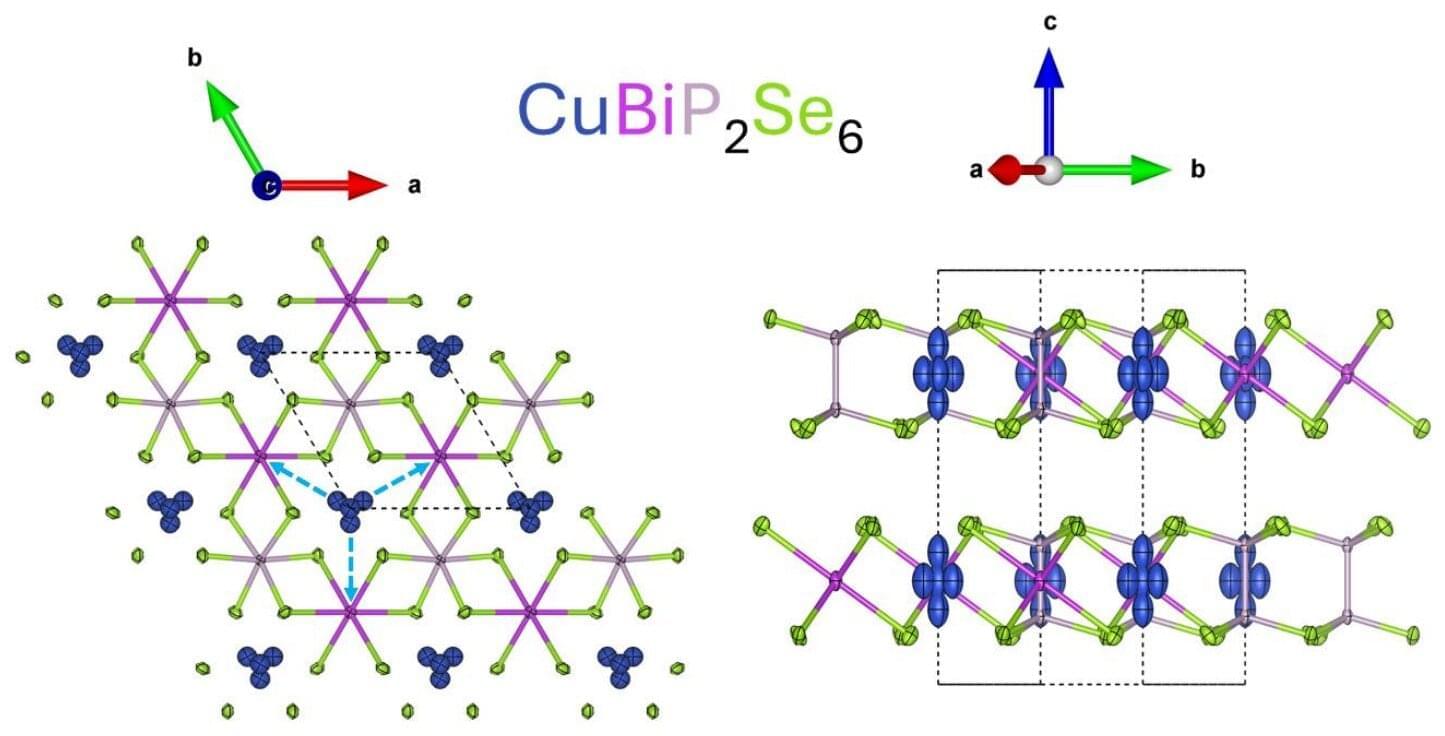
The research team, led by Peng Yan, a UMBC Ph.D. candidate in chemistry, and Joseph Bennett, assistant professor of chemistry and biochemistry at UMBC, focused on a type of 2D material called van der Waals layered phosphochalcogenides. Some of these materials are ferroelectric, meaning they can hold an electric charge in a particular direction, and then the direction can be reversed on command—sort of like tiny, reversible batteries. Some ferroelectric materials are also magnetic, behaving similarly when a magnetic field is applied. That combination makes them ideal for advanced electronics like memory devices and sensors.