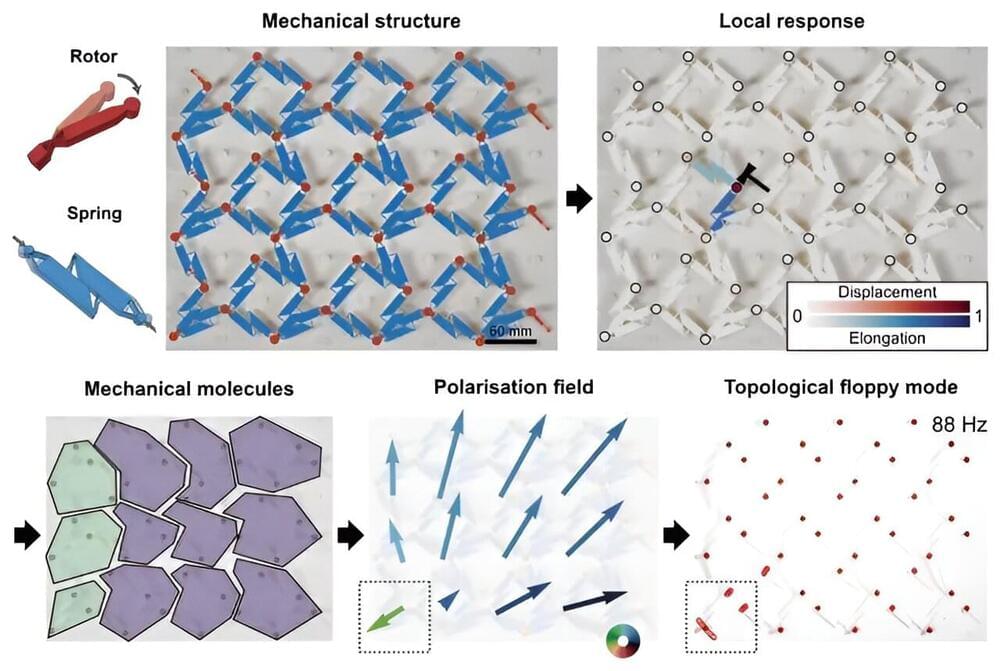
The branch of mathematics known as topology has become a cornerstone of modern physics thanks to the remarkable—and above all reliable—properties it can impart to a material or system. Unfortunately, identifying topological systems, or even designing new ones, is generally a tedious process that requires exactly matching the physical system to a mathematical model.
Researchers at the University of Amsterdam and the École Normale Supérieure of Lyon have demonstrated a model-free method for identifying topology, enabling the discovery of new topological materials using a purely experimental approach. The research is published in the journal Proceedings of the National Academy of Sciences.
Topology encompasses the properties of a system that cannot be changed by any “smooth deformation.” As you might be able to tell from this rather formal and abstract description, topology began its life as a branch of mathematics. However, over the last few decades physicists have demonstrated that the mathematics underlying topology can have very real consequences. Topological effects can be found in a wide range of physical systems, from individual electrons to large-scale ocean currents.