Dr. Rumi Chunara: “Our system learns to recognize more subtle patterns that distinguish trees from grass, even in challenging urban environments.”
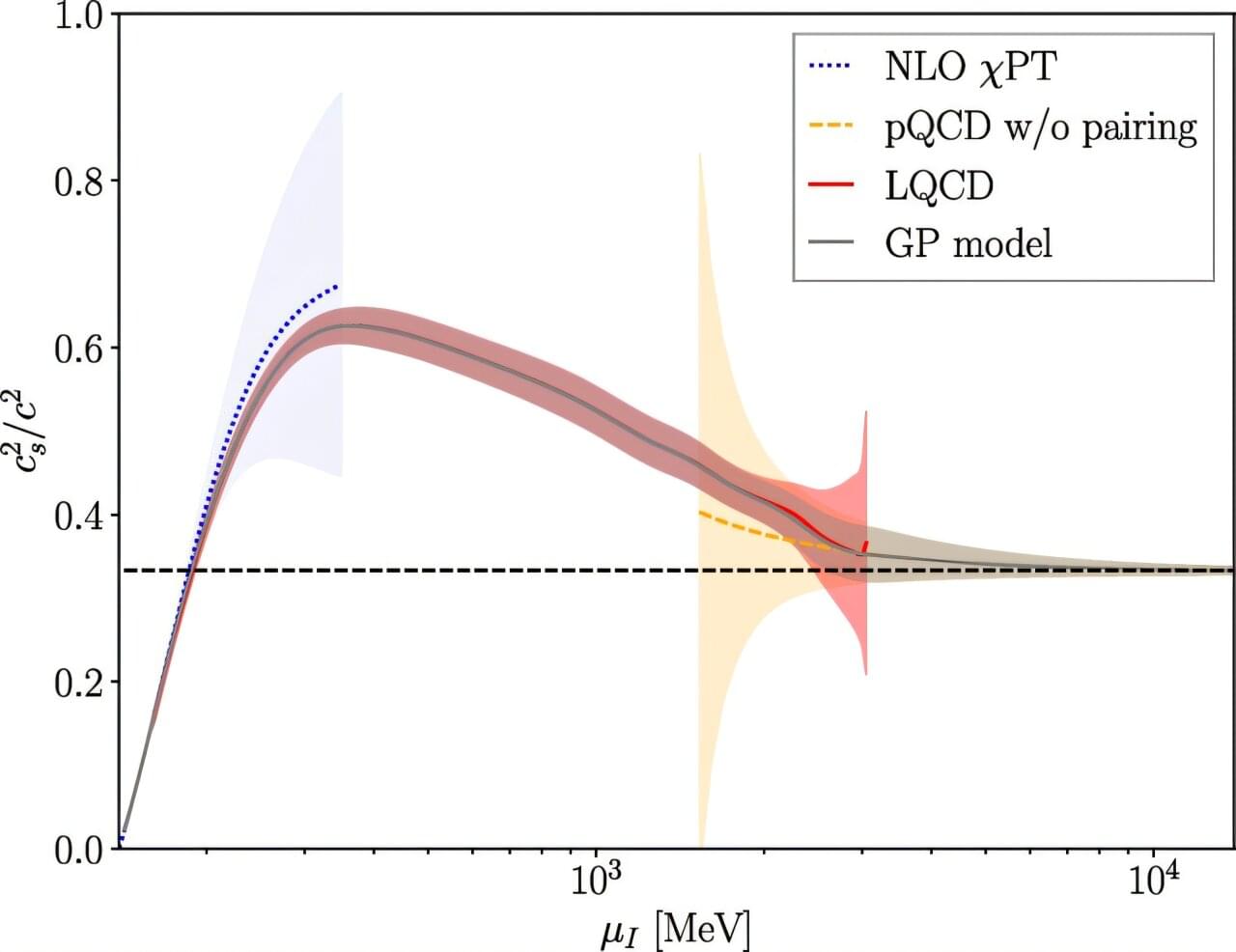
How can artificial intelligence (AI) help improve city planning to account for more green spaces? This is what a recent study published in the ACM Journal on Computing and Sustainable Societies hopes to address as a team of researchers proposed a novel concept using AI with the goal of both monitoring and improving urban green spaces, which are natural public spaces like parks and gardens, and provide a myriad of benefits, including physical and mental health, combating climate change, wildlife habitats, and increased social interaction.
For the study, the researchers developed a method they refer to as “green augmentation”, which uses an AI algorithm to analyze Google Earth satellite images with the goal of improving current AI methods by more accurately identifying green vegetation like grass and trees under various weather and seasonal conditions. For example, current AI methods identify green vegetation with an accuracy and reliability of 63.3 percent and 64 percent, respectively. Using this new method, the researchers successfully identified green vegetation with an accuracy and reliability of 89.4 percent and 90.6 percent, respectively.
“Previous methods relied on simple light wavelength measurements,” said Dr. Rumi Chunara, who is an associate professor of biostatistics at New York University and a co-author on the study. “Our system learns to recognize more subtle patterns that distinguish trees from grass, even in challenging urban environments. This type of data is necessary for urban planners to identify neighborhoods that lack vegetation so they can develop new green spaces that will deliver the most benefits possible. Without accurate mapping, cities cannot address disparities effectively.”