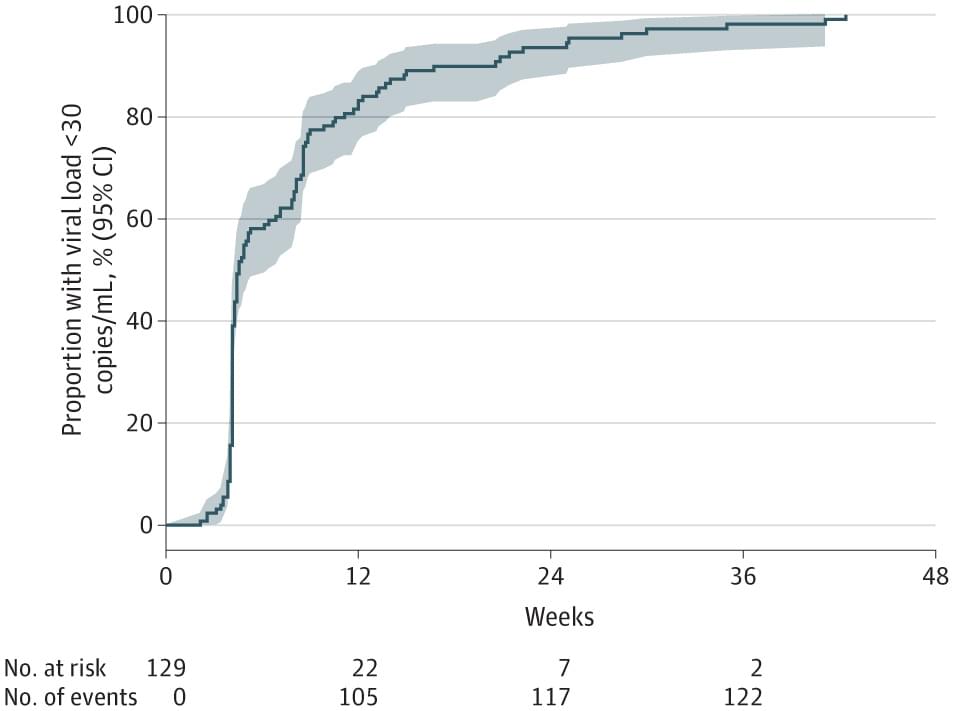
Durham University has contributed to new international research that critically assesses the intricate relationship between urban digitization and sustainability, focusing on the significant environmental impact of data centers.


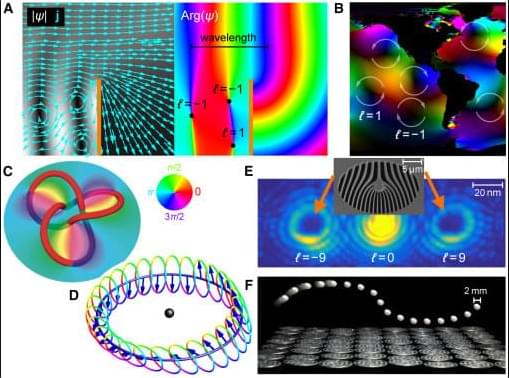
This commentary celebrates the 50th anniversary of the seminal paper by John F. Nye and Michael V. Berry published in 1974 that described topological wave singularities. Originally termed “wave dislocations,” they are now known as “wave vortices” and occur in diverse systems, such as tides, quantum matter waves, and most notably, light.

For years, Florida Tech’s Catherine Talbot, an assistant professor of psychology, has worked to understand the sociality of male rhesus monkeys and how low-social monkeys can serve as a model for humans with autism. Her most recent findings show that replenishing a deficient hormone, vasopressin, helped the monkeys become more social without increasing their aggression—a discovery that could change autism treatment.
Currently, the Centers for Disease Control and Prevention reports that one in 36 children in the United States is affected by autism spectrum disorder (ASD). That’s an increase from one in 44 children reported in 2018. Two FDA-approved treatments currently exist, Talbot said, but they only address associated symptoms, not the root of ASD. The boost in both prevalence and awareness of the disorder prompts the following question: What is the cause?
Some rhesus monkeys are naturally low-social, meaning they demonstrate poor social cognitive skills, while others are highly social. Their individual variation in sociality is comparable to how human sociality varies, ranging from people we consider social butterflies to those who are not interested in social interactions, similar to some people diagnosed with ASD, Talbot said. Her goal has been to understand how variations in biology and behavior influence social cognition.
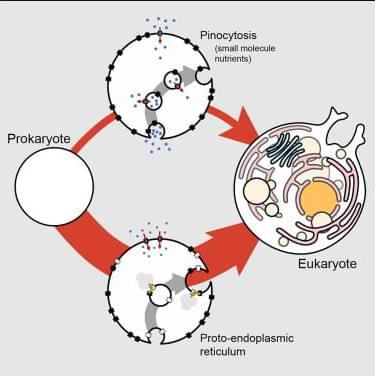
Schavemaker and Lynch derived functions that relate the cell biology of endomembranes to cellular fitness. Applied to the pinocytosis of small-molecule nutrients and the insertion of membrane proteins by a proto-endoplasmic reticulum, the proto-endoplasmic reticulum is revealed to be the more likely path to complex endomembranes in the origin of eukaryotes.
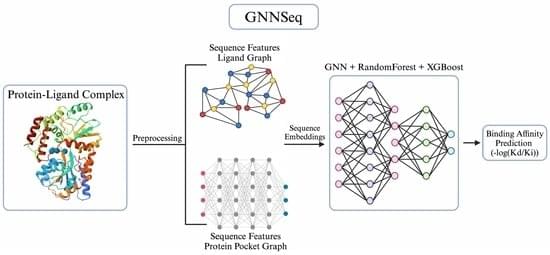
Background/Objectives: Accurately predicting protein–ligand binding affinity is essential in drug discovery for identifying effective compounds. While existing sequence-based machine learning models for binding affinity prediction have shown potential, they lack accuracy and robustness in pattern recognition, which limits their generalizability across diverse and novel binding complexes. To overcome these limitations, we developed GNNSeq, a novel hybrid machine learning model that integrates a Graph Neural Network (GNN) with Random Forest (RF) and XGBoost. Methods: GNNSeq predicts ligand binding affinity by extracting molecular characteristics and sequence patterns from protein and ligand sequences. The fully optimized GNNSeq model was trained and tested on subsets of the PDBbind dataset. The novelty of GNNSeq lies in its exclusive reliance on sequence features, a hybrid GNN framework, and an optimized kernel-based context-switching design. By relying exclusively on sequence features, GNNSeq eliminates the need for pre-docked complexes or high-quality structural data, allowing for accurate binding affinity predictions even when interaction-based or structural information is unavailable. The integration of GNN, XGBoost, and RF improves GNNSeq performance by hierarchical sequence learning, handling complex feature interactions, reducing variance, and forming a robust ensemble that improves predictions and mitigates overfitting. The GNNSeq unique kernel-based context switching scheme optimizes model efficiency and runtime, dynamically adjusts feature weighting between sequence and basic structural information, and improves predictive accuracy and model generalization. Results: In benchmarking, GNNSeq performed comparably to several existing sequence-based models and achieved a Pearson correlation coefficient (PCC) of 0.784 on the PDBbind v.2020 refined set and 0.84 on the PDBbind v.2016 core set. During external validation with the DUDE-Z v.2023.06.20 dataset, GNNSeq attained an average area under the curve (AUC) of 0.74, demonstrating its ability to distinguish active ligands from decoys across diverse ligand–receptor pairs. To further evaluate its performance, we combined GNNSeq with two additional specialized models that integrate structural and protein–ligand interaction features. When tested on a curated set of well-characterized drug–target complexes, the hybrid models achieved an average PCC of 0.89, with the top-performing model reaching a PCC of 0.97. GNNSeq was designed with a strong emphasis on computational efficiency, training on 5000+ complexes in 1 h and 32 min, with real-time affinity predictions for test complexes. Conclusions: GNNSeq provides an efficient and scalable approach for binding affinity prediction, offering improved accuracy and generalizability while enabling large-scale virtual screening and cost-effective hit identification. GNNSeq is publicly available in a server-based graphical user interface (GUI) format.