Artificial consciousness is inevitable, says new study. Mathematical model unifies theories and paves the way for sentient robots.


Metaphysics and the Matter with Things: Thinking with Iain McGilchrist was a collaborative conference put on by the Center for Process Studies (CPS) and the California Institute of Integral Studies (CIIS) in March of 2024. This three-day conference brought leading process thinkers across various disciplines, including physics, neuroscience, psychology, philosophy, and theology into critical dialogue with McGilchrist’s work in a collegial effort to assess, question, extend, and apply it. For more information on the conference and to purchase recordings, please visit https://ctr4process.org/mcgilchrist-conference/
Potential therapies could include precise genetic targeting of the GLUT4 pathway or dietary modifications to fine-tune glucose levels, ensuring an optimal environment for neurogenesis.
Stanford research uncovers glucose’s role in boosting neurogenesis, offering insights into brain aging interventions.

HEPS will transform scientific research by enabling high-energy X-ray probing at the nanoscale.
China is poised to unveil its cutting-edge High Energy Photon Source (HEPS) by year’s end, boasting some of the world’s most powerful synchrotron X-rays.
With a staggering investment of 4.8 billion yuan (approximately US$665 million), this facility marks a significant milestone for Asia, propelling China into the elite league of nations with fourth-generation synchrotron light sources.
Situated in Huairou, near downtown Beijing, the circular HEPS facility is a hive of activity as researchers meticulously calibrate thousands of components. These efforts are geared towards creating a light source capable of delving deep into samples, unveiling their molecular and atomic structures in real-time.

What if humans were an advanced, galactic civilization? Join us… and find out!Subscribe: https://wmojo.com/unveiled-subscribeIn this video, Unveiled takes…
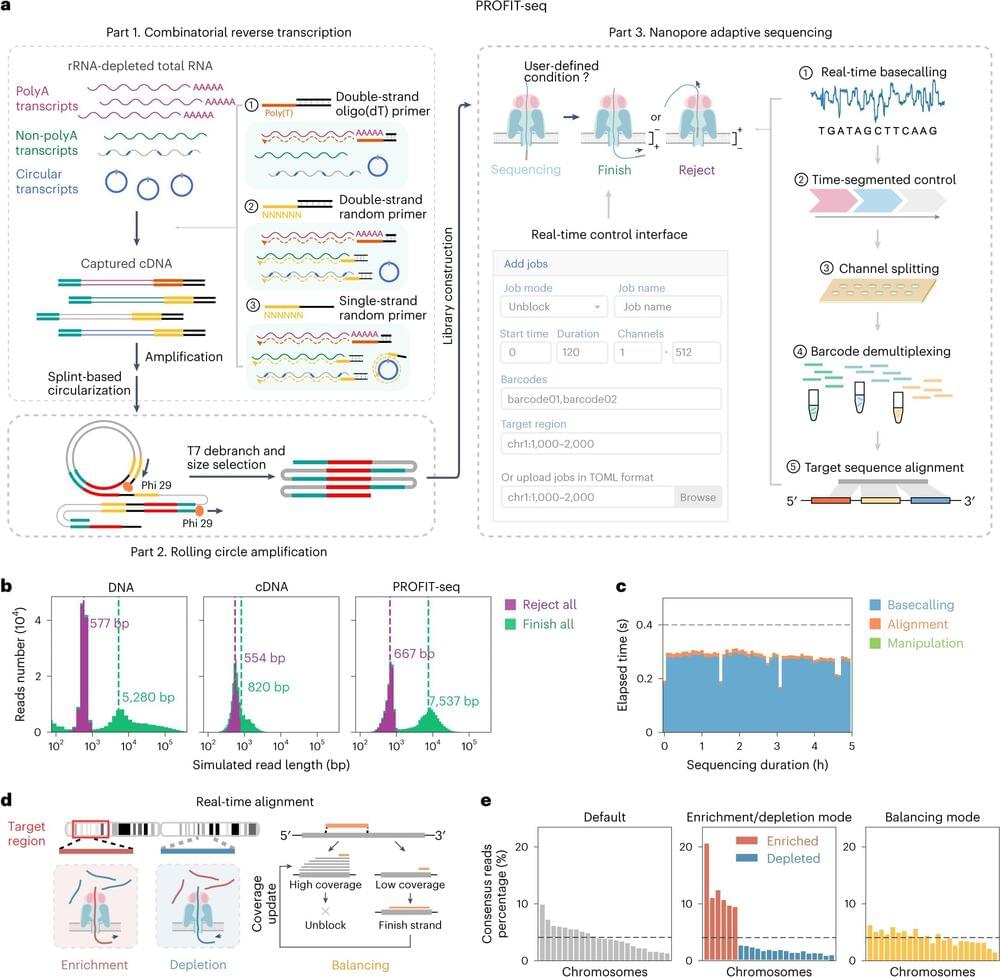
The high complexity and diversity of the eukaryotic transcriptome poses significant challenges for the efficient detection of specific transcripts. Conventional targeted RNA-seq methods often require labor-intensive pre-sequencing enrichment steps, which can compromise comprehensive transcriptome profiling and limit their broader applications.

A new type of wood is challenging our understanding of trees. The tulip tree (Liriodendron tulipifera) may significantly contribute to carbon management thanks to its wood, which is neither hard nor soft.
The discovery, named “midwood,” offers a way to improve CO₂ capture from the atmosphere. How could this wood change the game?
This solar breakthrough just changed everything.
Thanks to Opera for sponsoring this video. Click here https://opr.as/Opera-browser-DrBenMiles to upgrade your browser for FREE!
Last month, Oxford PV’s breakthrough solar cell broke the efficiency world record and is the world’s first commercially available Perovskite solar panel.
How does it work? And what does this mean for the future of solar?
Thanks you so much to the team for allowing me behind the scenes into their development facility and for the free Halloween costume.
#solar #efficiency #breakthrough #physics #perovskite.
Chapters.
0:00 The Solar Power Breakthrough.
3:25 Humanity’s Journey to Capture the Sun.
8:46 How We Broke the Limit of Solar Efficiency.
13:15 Building the World’s First Perovskite Solar Panel.
17:23 The Future of Solar.
🚀 JOIN US for members-only content: https://www.patreon.com/DrBenMiles.