A conversation with Marinka Zitnik, assistant professor of biomedical informatics in the Blavatnik Institute at HMS


A conversation with Marinka Zitnik, assistant professor of biomedical informatics in the Blavatnik Institute at HMS
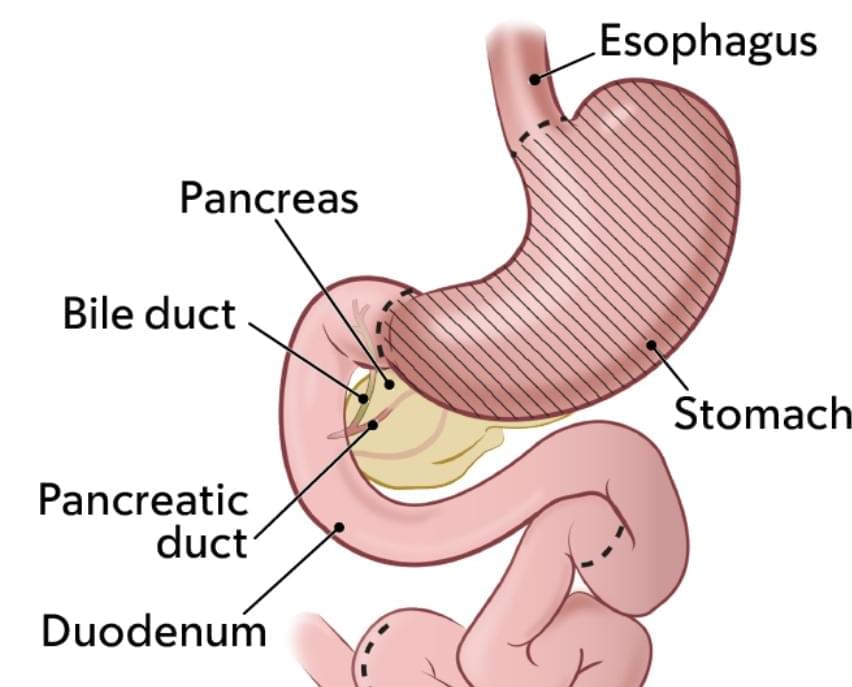
In a recent study, more than 90% of participants whose stomachs had been surgically removed to prevent cancer experienced a least one chronic complication 2 years out from their surgery. For some, the complications are life-altering.
Findings from a recent study will help clinicians counsel people who are considering preventive gastrectomy about the long-term impacts of the surgery.
Chinese automaker GAC unveils its third-gen self-developed humanoid robot, showcasing motion control, navigation, and AI capabilities.

Students learning quantum mechanics are taught the Schrodinger equation and how to solve it to obtain a wave function. But a crucial step is skipped because it has puzzled scientists since the earliest days—how does the real, classical world emerge from, often, a large number of solutions for the wave functions?
Each of these wave functions has its individual shape and associated energy level, but how does the wave function “collapse” into what we see as the classical world—atoms, cats and the pool noodles floating in the tepid swimming pool of a seedy hotel in Las Vegas hosting a convention of hungover businessmen trying to sell the world a better mousetrap?
At a high level, this is handled by the “Born rule”—the postulate that the probability density for finding an object at a particular location is proportional to the square of the wave function at that position.

Exploiting an ingenious combination of photochemical (i.e., light-induced) reactions and self-assembly processes, a team led by Prof. Alberto Credi of the University of Bologna has succeeded in inserting a filiform molecule into the cavity of a ring-shaped molecule, according to a high-energy geometry that is not possible at thermodynamic equilibrium. In other words, light makes it possible to create a molecular “fit” that would otherwise be inaccessible.
“We have shown that by administering light energy to an aqueous solution, a molecular self-assembly reaction can be prevented from reaching a thermodynamic minimum, resulting in a product distribution that does not correspond to that observed at equilibrium,” says Alberto Credi.
“Such a behavior, which is at the root of many functions in living organisms, is poorly explored in artificial molecules because it is very difficult to plan and observe. The simplicity and versatility of our approach, together with the fact that visible light—i.e., sunlight—is a clean and sustainable energy source, allow us to foresee developments in various areas of technology and medicine.”

Combining metallic glass with the Berreman mode of epsilon-near-zero (ENZ) thin films achieves a dual-function system for infrared camouflage and thermal management within an identical wavelength region of the atmospheric window. In recent research, metallic glasses were selected for their tunable optical properties, providing adjustable emissivity for versatile thermal camouflage while maintaining effective thermal management.
Thermal infrared camouflage aims to reduce the detectability of a target using thermal imaging devices. Given the typically high thermal emissivity in everyday environments, the thermal emissivity of the background environment must be considered. The conventional low-emissivity strategy for thermal camouflage is only effective for targets at extremely high temperatures, making it unsuitable for applications near room-to-medium-high temperature range (350 °C).
In a study published in Materials Horizons, Professor Hsuen-Li Chen from the Department of Materials Science and Engineering at National Taiwan University led his research team in designing an innovative multilayer thin-film structure. This structure introduces metallic glass into infrared thermal camouflage technology, exploiting its adjustable emissivity to accommodate diverse infrared thermal camouflage scenarios.

Optical tweezers and related techniques provide extraordinary opportunities for research and applications in the physical, biological, and medical fields. However, certain requirements such as high-intensity laser beams, sophisticated electrode designs, additional electric sources, and low-conductive media, significantly impede their flexibility and adaptability, thus hindering their practical applications.
In a study published in The Innovation, a research team led by Dr. Du Xuemin from the Shenzhen Institutes of Advanced Technology (SIAT) of the Chinese Academy of Sciences reported a novel photopyroelectric tweezer (PPT) that combines the advantages of the light and electric fields. The PPT enables versatile manipulation in various working scenarios.
The proposed PPT consists of two key components, a near infrared (NIR) spectrum laser light source and a PPT device that includes a liquid medium and a photopyroelectric substrate.

Racing closer to the Sun than ever before, the Parker Solar Probe is unlocking the secrets of our solar system’s fiery heart.
NASAs Parker Solar Probe has successfully transmitted a beacon signal back to Earth, confirming it is in good health and functioning normally after its record-breaking close approach to the Sun.
The mission operations team at Johns Hopkins Applied Physics Laboratory (APL) in Laurel, Maryland, received the signal just before midnight EST on December 26. During its closest approach on December 24, the spacecraft traveled at an astonishing 430,000 miles per hour and came within 3.8 million miles of the Sun’s surface, making it the closest any human-made object has ever been to our star.

An international team of scientists, led by Dr. Lukas Bruder, a junior research group leader at the University of Freiburg’s Institute of Physics, has successfully created and controlled hybrid electron-photon quantum states in helium atoms.
The team accomplished this by generating specially designed, highly intense extreme ultraviolet light pulses using the FERMI free electron laser in Trieste, Italy. By employing an innovative laser pulse-shaping technique, they were able to precisely control these hybrid quantum states. The groundbreaking findings have been published in Nature.