Tests of large language models reveal that they can behave in deceptive and potentially harmful ways. What does this mean for the future?


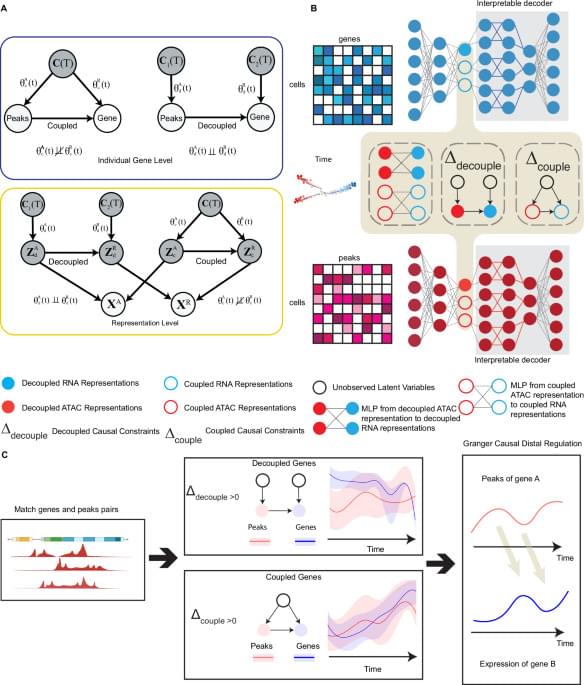
Chromatin accessibility dynamics causally influence changes in gene expression levels, but these fluctuations may not be directly coupled over time. Here, authors develop computational causal framework HALO, examining epigenetic plasticity and gene regulation dynamics in single-cell multi-omic data.

Computational Creativity, Concept Invention, and General Intelligence in their own right all are flourishing research disciplines producing surprising and captivating results that continuously influence and change our view on where the limits of intelligent machines lie, each day pushing the boundaries a bit further. By 2014, all three fields also have left their marks on everyday life – machine-composed music has been performed in concert halls, automated theorem provers are accepted tools in enterprises’ R&D departments, and cognitive architectures are being integrated in pilot assistance systems for next generation airplanes.



This book is a collection of writings by active researchers in the field of Artificial General Intelligence, on topics of central importance in the field. Each chapter focuses on one theoretical problem, proposes a novel solution, and is written in sufficiently non-technical language to be understandable by advanced undergraduates or scientists in allied fields.
This book is the very first collection in the field of Artificial General Intelligence (AGI) focusing on theoretical, conceptual, and philosophical issues in the creation of thinking machines. All the authors are researchers actively developing AGI projects, thus distinguishing the book from much of the theoretical cognitive science and AI literature, which is generally quite divorced from practical AGI system building issues.
Go to https://ground.news/sabine to get 40% off the Vantage plan and see through sensationalized reporting. Stay fully informed on events around the world with Ground News.
Over the past few decades, the idea that gravity is not a fundamental interaction but is instead caused by the increase of entropy has become increasingly popular in the world of physics. Today, we have a paper from a group of physicists who claim that entropic gravity might be the result of space being full of qubits. Let’s take a look.
Paper: https://journals.aps.org/prx/abstract… Check out my new quiz app ➜ http://quizwithit.com/ 📚 Buy my book ➜ https://amzn.to/3HSAWJW 💌 Support me on Donorbox ➜ https://donorbox.org/swtg 📝 Transcripts and written news on Substack ➜ https://sciencewtg.substack.com/ 👉 Transcript with links to references on Patreon ➜ / sabine 📩 Free weekly science newsletter ➜ https://sabinehossenfelder.com/newsle… 👂 Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl… 🔗 Join this channel to get access to perks ➜
/ @sabinehossenfelder #science #sciencenews #physics #gravity.
🤓 Check out my new quiz app ➜ http://quizwithit.com/
📚 Buy my book ➜ https://amzn.to/3HSAWJW
💌 Support me on Donorbox ➜ https://donorbox.org/swtg.
📝 Transcripts and written news on Substack ➜ https://sciencewtg.substack.com/
👉 Transcript with links to references on Patreon ➜ / sabine.
📩 Free weekly science newsletter ➜ https://sabinehossenfelder.com/newsle…
👂 Audio only podcast ➜ https://open.spotify.com/show/0MkNfXl…
🔗 Join this channel to get access to perks ➜
/ @sabinehossenfelder.
#science #sciencenews #physics #gravity

The prevalence of Alzheimer’s disease (AD) is approximately two times higher in African Americans (AA) compared to white/European-ancestry (EA) individuals living in the U.S. Some of this is due to social determinants of health such as disparities in health care access and quality of education, biases in testing and higher rates of AD risk factors such as cardiovascular disease and diabetes in those who identify as African American.
Although many studies have examined differences in gene expression (a measure of the amount of protein encoded by a gene) in brain tissue from AD cases and controls in EA or mixed ancestry cohorts, the number of AA individuals in these studies was unspecified or too small to identify significant findings within this group alone.
In the largest AD study conducted in brain tissue from AA donors, researchers from Boston University Chobanian & Avedisian School of Medicine have identified many genes, a large portion of which had not previously been implicated in AD by other genetic studies, to be significantly more or less active in tissue from AD cases compared to controls. The most notable finding was a 1.5 fold higher level of expression of the ADAMTS2 gene in brain tissue from those with autopsy-confirmed AD.