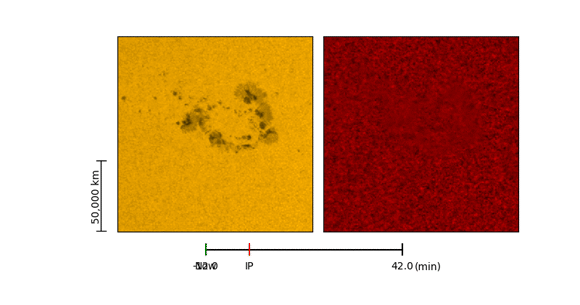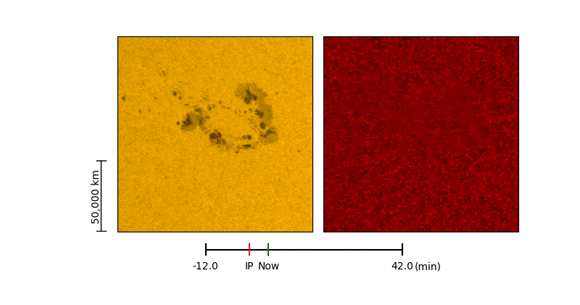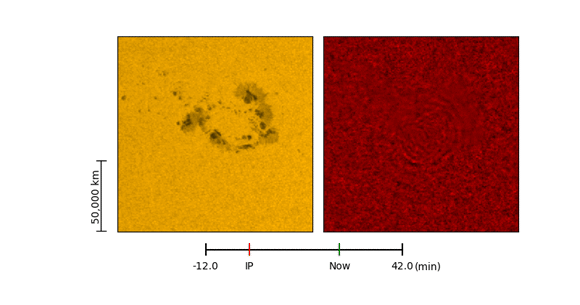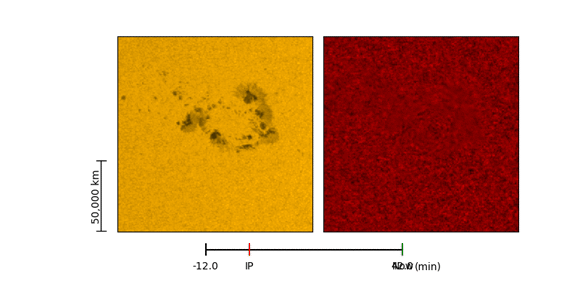
Ultra-impulsive acoustic emission from a solar flare recently detected by NASA’s Solar Dynamics Observatory (SDO) indicated submersion of its source beneath the active region that hosted the flare.


By Hubble Resembles Reputed “Planet Nine” in Our Solar System.
Astronomers confirm bound orbit for planet far from its star, showing that far-flung planets exist.
Astronomers are still searching for a hypothetical “Planet Nine” in the distant reaches of our solar system, but an exoplanet 336 light years from Earth is looking more and more like the Planet Nine of its star system.
Planet Nine, potentially 10 times the size of Earth and orbiting far beyond Neptune in a highly eccentric orbit about the sun, was proposed in 2012 to explain perturbations in the orbits of dwarf planets just beyond Neptune’s orbit, so-called detached Kuiper Belt objects. It has yet to be found, if it exists.

NASA’s Lucy mission is one step closer to launch as L’TES, the Lucy Thermal Emission Spectrometer, has been successfully integrated on to the spacecraft.
“Having two of the three instruments integrated onto the spacecraft is an exciting milestone,” said Donya Douglas-Bradshaw, Lucy project manager from NASA’s Goddard Space Flight Center in Greenbelt, Maryland. “The L’TES team is to be commended for their true dedication and determination.”
Lucy will be the first space mission to study the Trojan asteroids, leftover building blocks of the Solar System’s outer planets orbiting the Sun at the distance of Jupiter. The mission takes its name from the fossilized human ancestor (called “Lucy” by her discoverers) whose skeleton provided unique insight into humanity’s evolution. Likewise, the Lucy mission will revolutionize our knowledge of planetary origins and the birth of our solar system more than 4 billion years ago.
The human eye is a surprisingly good photon detector. What can it spy of the line between the quantum and classical worlds?
I spent a lot of time in the dark in graduate school. Not just because I was learning the field of quantum optics – where we usually deal with one particle of light or photon at a time – but because my research used my own eyes as a measurement tool. I was studying how humans perceive the smallest amounts of light, and I was the first test subject every time.
I conducted these experiments in a closet-sized room on the eighth floor of the psychology department at the University of Illinois, working alongside my graduate advisor, Paul Kwiat, and psychologist Ranxiao Frances Wang. The space was equipped with special blackout curtains and a sealed door to achieve total darkness. For six years, I spent countless hours in that room, sitting in an uncomfortable chair with my head supported in a chin rest, focusing on dim, red crosshairs, and waiting for tiny flashes delivered by the most precise light source ever built for human vision research. My goal was to quantify how I (and other volunteer observers) perceived flashes of light from a few hundred photons down to just one photon.
As individual particles of light, photons belong to the world of quantum mechanics – a place that can seem totally unlike the Universe we know. Physics professors tell students with a straight face that an electron can be in two places at once (quantum superposition), or that a measurement on one photon can instantly affect another, far-away photon with no physical connection (quantum entanglement). Maybe we accept these incredible ideas so casually because we usually don’t have to integrate them into our daily existence. An electron can be in two places at once; a soccer ball cannot.


A membrane between what is inside the solar system and the outside. 😃
NASA‘s New Horizons spacecraft has helped scientists study a mysterious phenomenon at the edge of the Solar System, where particles from the Sun and interstellar space interact.
This region, about 100 times further from the Sun than Earth, is where uncharged hydrogen atoms from interstellar space meet charged particles from our Sun. The latter extend out from our Sun in a bubble called the heliosphere.
At the point where the two interact, known as the heliopause, it’s thought there is a build-up of hydrogen from interstellar space. This creates a sort of “wall”, which scatters incoming ultraviolet light.
Circa2016 photonic propulsion.
There’s no argument in the astronomical community—rocket-propelled spacecraft can take us only so far. The SLS will likely take us to Mars, and future rockets might be able to help us reach even more distant points in the solar system. But Voyager 1 only just left the solar system, and it was launched in 1977. The problem is clear: we cannot reach other stars with rocket fuel. We need something new.
“We will never reach even the nearest stars with our current propulsion technology in even 10 millennium,” writes Physics Professor Philip Lubin of the University of California Santa Barbara in a research paper titled A Roadmap to Interstellar Flight. “We have to radically rethink our strategy or give up our dreams of reaching the stars, or wait for technology that does not exist.”
Lubin received funding from NASA last year to study the possibility of using photonic laser thrust, a technology that does exist, as a new system to propel spacecraft to relativistic speeds, allowing them to travel farther than ever before. The project is called DEEP IN, or Directed Propulsion for Interstellar Exploration, and the technology could send a 100-kg (220-pound) probe to Mars in just three days, if research models are correct. A much heavier, crewed spacecraft could reach the red planet in a month—about a fifth of the time predicted for the SLS.

An international team of astronomers has investigated a nearby emission nebula and star-forming region dubbed the Cat’s Paw Nebula as part of the B-field In STar-forming Region Observations (BISTRO) survey. Results of this study, presented in a paper published December 24 on arXiv.org, provide essential information about the structure of the object’s complex magnetic field.
At a distance of some 4240 light years away, the Cat’s Paw Nebula (other designations: NGC 6334, Gum 64) is a high-mass star-forming complex that lies within the galactic plane. The nebula has a form of a filamentary cloud structure spanning 1000 light years and hosts several star-forming regions.
Observations show that NGC 6334 is dominated by both a dense ridge threaded by sub-filaments, and by two hub-like structures towards its Northeast end. Astronomers have found that this ridge itself is in the process of active high-mass star formation and ultra-compact HII regions, maser sources, and molecular outflows have been identified along or next to its crest. However, although column density and velocity structures of the nebula’s both filaments and hubs have been thoroughly studied, still very little is known about its magnetic field (B-field).

The Orion is a sub-orbital electric aircraft equipped with an air-breathing magneto-plasma jet propulsion engine that could go from the tarmac to an altitude of 24000 metres and cruise at about 800 km/h.
It would bring passengers to the edge of black space with stunning views from its ultra-wide panoramic windows. Its new plasma pulse detonation engine could become the standard of this nascent industry.
It’s obvious that sub-orbital jets will become in demand as Earth’s population and wealth continues to rise. There’s already a lot of demand for jets capable of reaching this kind of altitude, but one major barrier has been the engine’s performance and overall costs. The Orion concept is all about introducing a new type of propulsion (plasma jet) and seeing how it could benefit various industries.

O,.o kaons in action for interstellar travel: D.
Interstellar probes and future interstellar travel will require relativistic rockets. The problem is that such a rocket drive requires that the rocket exhaust velocity from the fuel also is relativistic, since otherwise the rocket thrust is much too small: the total mass of the fuel will be so large that relativistic speeds cannot be reached in a reasonable time and the total mass of the rocket will be extremely large. Until now, no technology was known that would be able to give rocket exhaust at relativistic speed and a high enough momentum for relativistic travel. Here, a useful method for relativistic interstellar propulsion is described for the first time. This method gives exhaust at relativistic speeds and is a factor of at least one hundred better than normal fusion due to its increased energy output from the annihilation-like meson formation processes. It uses ordinary hydrogen as fuel so a return travel is possible after refuelling almost anywhere in space. The central nuclear processes have been studied in around 20 publications, which is considered to be sufficient evidence for the general properties. The nuclear processes give relativistic particles (kaons, pions and muons) by laser-induced annihilation-like processes in ultra-dense hydrogen H. The kinetic energy of the mesons is 1300 times larger than the energy of the laser pulse. This method is superior to the laser-sail method by several orders of magnitude and is suitable for large spaceships.