Some numbers are so unimaginably large that they defy the bounds of modern mathematics, and now mathematicians are closing in on a number that may mark the edge of this bizarre abyss


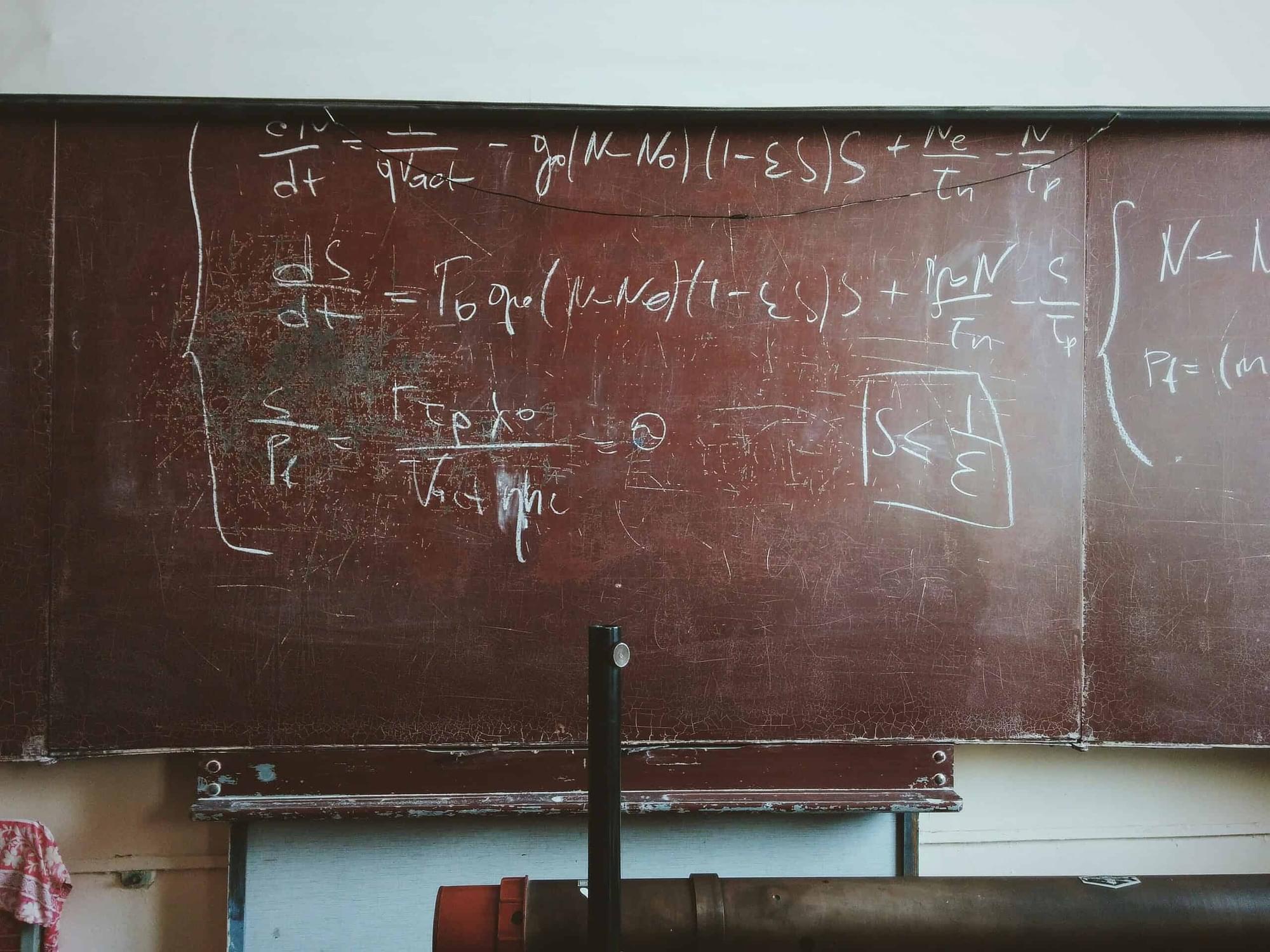

D.P. Kroese, Z.I. Botev, T. Taimre, R. Vaisman. Data Science and Machine Learning: Mathematical and Statistical Methods, Chapman and Hall/CRC, Boca Raton, 2019.
The purpose of this book is to provide an accessible, yet comprehensive textbook intended for students interested in gaining a better understanding of the mathematics and statistics that underpin the rich variety of ideas and machine learning algorithms in data science.

Inspired by the “Harry Potter” stories and the Disney Channel show “Wizards of Waverly Place,” 7-year-old Sabrina Corsetti emphatically declared to her parents one afternoon that she was, in fact, a wizard.
“My dad turned to me and said that, if I really wanted to be a wizard, then I should become a physicist. Physicists are the real wizards of the world,” she recalls.
That conversation stuck with Corsetti throughout her childhood, all the way up to her decision to double-major in physics and math in college, which set her on a path to MIT, where she is now a graduate student in the Department of Electrical Engineering and Computer Science.
While her work may not involve incantations or magic wands, Corsetti’s research centers on an area that often produces astonishing results: integrated photonics. A relatively young field, integrated photonics involves building computer chips that route light instead of electricity, enabling compact and scalable solutions for applications ranging from communications to sensing.
MIT graduate student Sabrina Corsetti is exploring the cutting edge of integrated photonics, which involves building computer chips that route light instead of electricity. Her projects have included a chip-sized 3D printer and miniaturized optical systems for quantum computing.
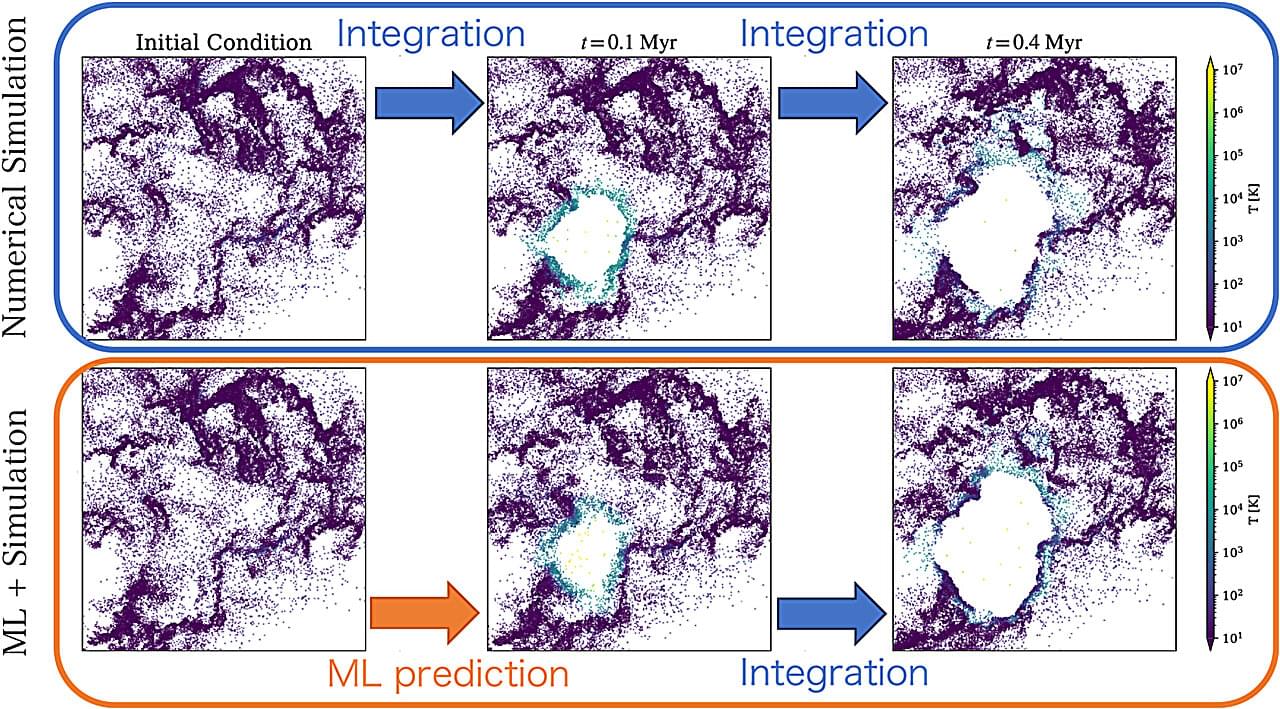
Researchers have used machine learning to dramatically speed up the processing time when simulating galaxy evolution coupled with supernova explosion. This approach could help us understand the origins of our own galaxy, particularly the elements essential for life in the Milky Way.
The findings are published in The Astrophysical Journal.
The team was led by Keiya Hirashima at the RIKEN Center for Interdisciplinary Theoretical and Mathematical Sciences (iTHEMS) in Japan, along with colleagues from the Max Planck Institute for Astrophysics (MPA) and the Flatiron Institute.

Meta’s Superintelligence Lab has assembled a world-class team of AI researchers from institutions like OpenAI, DeepMind, and Google. Their educational paths—often beginning in top universities in China or India and leading to elite Western institutions—reflect the global and interdisciplinary nature of AGI development. This article explores their academic journeys, highlighting how rigorous training in mathematics, computer science, and safety research underpins the next frontier of artificial intelligence.
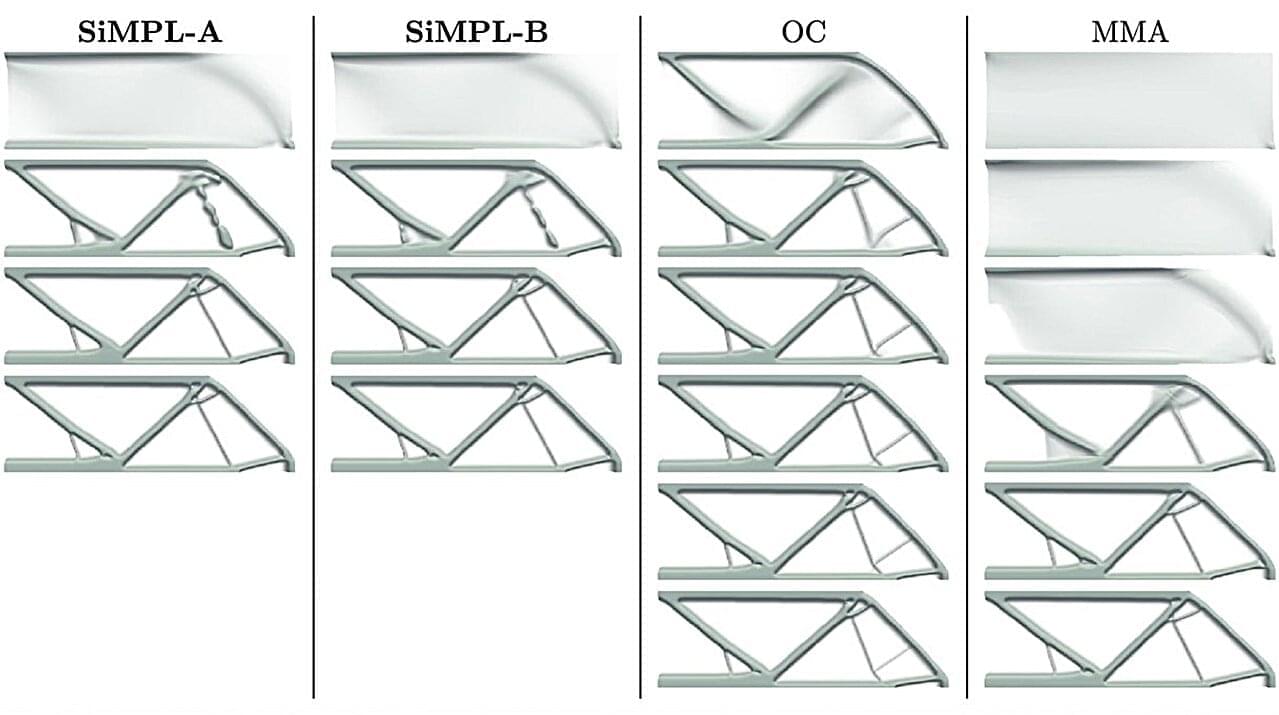
With the rise of 3D printing and other advanced manufacturing methods, engineers can now build structures that were once impossible to fabricate. An emerging design strategy that takes full advantage of these new capabilities is topology optimization—a computer-driven technique that determines the most effective way to distribute material, leading to an optimized design.
Now, a research team including mathematicians from Brown University has developed a new approach that dramatically improves the speed and stability of topology optimization algorithms. The team, a collaboration between researchers at Brown, Lawrence Livermore National Laboratory and Simula Research Laboratory in Norway, detailed their work in two recently published papers in the SIAM Journal on Optimization and Structural and Multidisciplinary Optimization.
“Our method beats some existing methods by four or five times in terms of efficiency,” said Brendan Keith, an assistant professor of applied mathematics at Brown. “That’s a huge computational savings that could enable people to make designs more quickly and inexpensively, or to develop more complex designs with higher resolution.”
Satyendra Nath Bose FRS, MP [ 1 ] (/ ˈ b oʊ s / ; [ 4 ] [ a ] 1 January 1894 – 4 February 1974) was an Indian theoretical physicist and mathematician. He is best known for his work on quantum mechanics in the early 1920s, in developing the foundation for Bose–Einstein statistics, and the theory of the Bose–Einstein condensate. A Fellow of the Royal Society, he was awarded India’s second highest civilian award, the Padma Vibhushan, in 1954 by the Government of India. [ 5 ] [ 6 ] [ 7 ]
The eponymous particles class described by Bose’s statistics, bosons, were named by Paul Dirac. [ 8 ] [ 9 ]
A polymath, he had a wide range of interests in varied fields, including physics, mathematics, chemistry, biology, mineralogy, philosophy, arts, literature, and music. He served on many research and development committees in India, after independence. [ 10 ] .

How reliable is artificial intelligence, really? An interdisciplinary research team at TU Wien has developed a method that allows for the exact calculation of how reliably a neural network operates within a defined input domain. In other words: It is now possible to mathematically guarantee that certain types of errors will not occur—a crucial step forward for the safe use of AI in sensitive applications.
From smartphones to self-driving cars, AI systems have become an everyday part of our lives. But in applications where safety is critical, one central question arises: Can we guarantee that an AI system won’t make serious mistakes—even when its input varies slightly?
A team from TU Wien—Dr. Andrey Kofnov, Dr. Daniel Kapla, Prof. Efstathia Bura and Prof. Ezio Bartocci—bringing together experts from mathematics, statistics and computer science, has now found a way to analyze neural networks, the brains of AI systems, in such a way that the possible range of outputs can be exactly determined for a given input range—and specific errors can be ruled out with certainty.

Clocks might be far more fundamental to physics than we ever realized.
A new theory suggests what we see around us – from the smallest of quantum actions to the cosmic crawl of entire galaxies – could all be literally a matter of time. Three dimensions of time, in fact.
The basic idea of 3D time isn’t new. But University of Alaska geophysicist Gunther Kletetschka says his mathematical framework is the first to reproduce known properties of the Universe, making it a somewhat serious contender for uniting physics under one consistent model.