Researchers used mathematical modeling to analyze the movements of individual organisms that make up a coral, finding correlation between their otherwise random sways and bounces.


Watch over 2,400 documentaries for free for 30 days AND get a free Nebula account by signing up at https://curiositystream.com/upandatom and using the code “upandatom”. Once you sign up you’ll get an email about Nebula. If you don’t get one, contact the curiosity stream support team and they will set you up with a free Nebula account right away.
Nebula: https://watchnebula.com/
Hi! I’m Jade. If you’d like to consider supporting Up and Atom, head over to my Patreon page smile
https://www.patreon.com/upandatom.
Visit the Up and Atom store.
https://store.nebula.app/collections/up-and-atom.
*ALL THE LINKS*

An encryption tool co-created by a University of Cincinnati math professor will soon safeguard the telecommunications, online retail and banking and other digital systems we use every day.
The National Institute of Standards and Technology chose four new encryption tools designed to thwart the next generation of hackers or thieves. One of them, called CRYSTALS-Kyber, is co-created by UC College of Arts and Sciences math professor Jintai Ding.
“It’s not just for today but for tomorrow,” Ding said. “This is information that you don’t want people to know even 30 or 50 years from now.”
To try out our new course (and many others on math and science), go to https://brilliant.org/sabine. You can get started for free, and the first 200 will get 20% off the annual premium subscription.
Physicists have many theories for the beginning of our universe: A big bang, a big bounce, a black hole, a network, a collision of membranes, a gas of strings, and the list goes on. What does this mean? It means we don’t know how the universe began. And the reason isn’t just that we’re lacking data, the reason is that science is reaching its limits when we try to understand the initial condition of the entire universe.
💌 Sign up for my weekly science newsletter. It’s free! ➜ http://sabinehossenfelder.com/
👉 Support me on Patreon ➜ https://www.patreon.com/Sabine.
📖 My new book “Existential Physics” is now on sale ➜ http://existentialphysics.com/
🔗 Join this channel to get access to perks ➜
https://www.youtube.com/channel/UC1yNl2E66ZzKApQdRuTQ4tw/join.
The Poplawski paper about how the universe might have been born from a black hole is here: https://link.springer.com/article/10.1007/s10714-021-02790-7
00:00 Intro.
00:25 The Big Bang Theory.
03:47 Why So Many Other Theories?
04:53 The Problem With Cosmology.
07:30 The Importance of Simplicity.
10:57 Stories of Creation.
15:35 Sponsor Message


Mathematical models suggest that with just a few more genes, it might be possible to define hundreds of cellular identities, more than enough to populate the tissues of complex organisms. It’s a finding that opens the door to experiments that could bring us closer to understanding how, eons ago, the system that builds us was built.
The Limits of Mutual Repression
Developmental biologists have illuminated many tipping points and chemical signals that prompt cells to follow one developmental pathway or another by studying natural cells. But researchers in the field of synthetic biology often take another approach, explained Michael Elowitz, a professor of biology and bioengineering at Caltech and an author of the new paper: They build a system of cell-fate control from scratch to see what it can tell us about what such systems require.
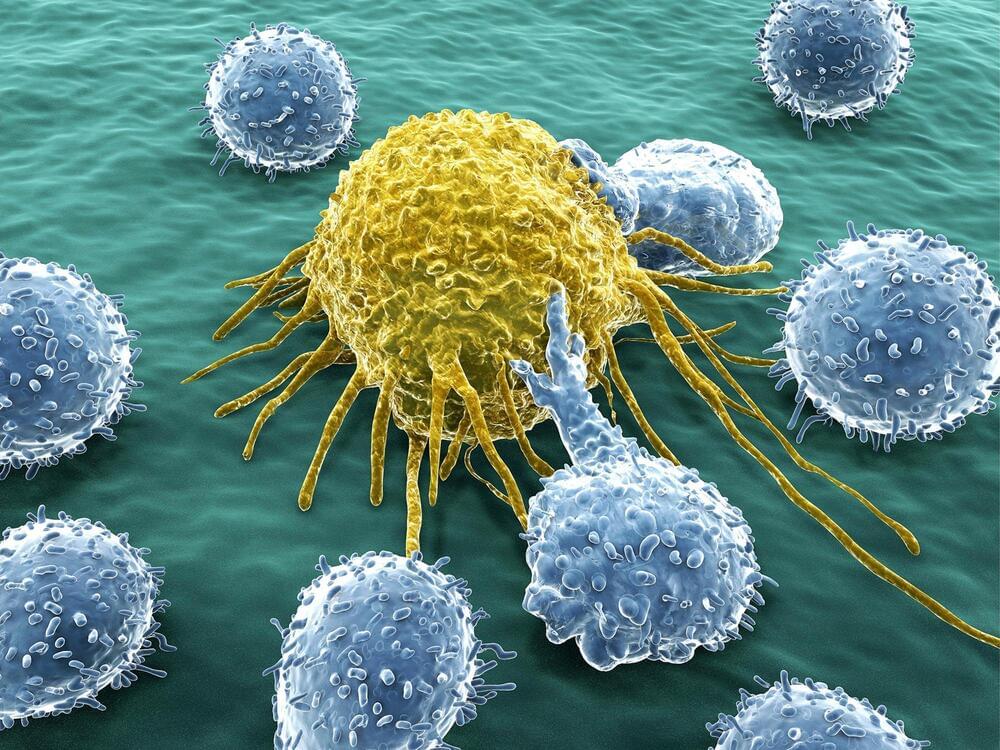
A new molecule created by a researcher at the University of Texas at Dallas kills a variety of difficult-to-treat cancers, including triple-negative breast cancer, by taking advantage of a weakness in cells that was not previously targeted by existing drugs.
The research, which was conducted using isolated cells, human cancer tissue, and mouse-grown human cancers, was recently published in Nature Cancer.
A co-corresponding author of the study and an associate professor of chemistry and biochemistry in the School of Natural Sciences and Mathematics at the University of Texas at Dallas, Dr. Jung-Mo Ahn has dedicated more than ten years of his career to developing small molecules that target protein-protein interactions in cells. He previously created potential therapeutic candidate compounds for treatment-resistant prostate cancer and breast cancer using a method called structure-based rational drug design.

Meta is developing a machine learning model that scans these citations and cross-references their content to Wikipedia articles to verify that not only the topics line up, but specific figures cited are accurate.
This isn’t just a matter of picking out numbers and making sure they match; Meta’s AI will need to “understand” the content of cited sources (though “understand” is a misnomer, as complexity theory researcher Melanie Mitchell would tell you, because AI is still in the “narrow” phase, meaning it’s a tool for highly sophisticated pattern recognition, while “understanding” is a word used for human cognition, which is still a very different thing).
Meta’s model will “understand” content not by comparing text strings and making sure they contain the same words, but by comparing mathematical representations of blocks of text, which it arrives at using natural language understanding (NLU) techniques.

Today, Oak Ridge National Laboratory’s Frontier supercomputer was crowned fastest on the planet in the semiannual Top500 list. Frontier more than doubled the speed of the last titleholder, Japan’s Fugaku supercomputer, and is the first to officially clock speeds over a quintillion calculations a second—a milestone computing has pursued for 14 years.
That’s a big number. So before we go on, it’s worth putting into more human terms.
Imagine giving all 7.9 billion people on the planet a pencil and a list of simple arithmetic or multiplication problems. Now, ask everyone to solve one problem per second for four and half years. By marshaling the math skills of the Earth’s population for a half-decade, you’ve now solved over a quintillion problems.
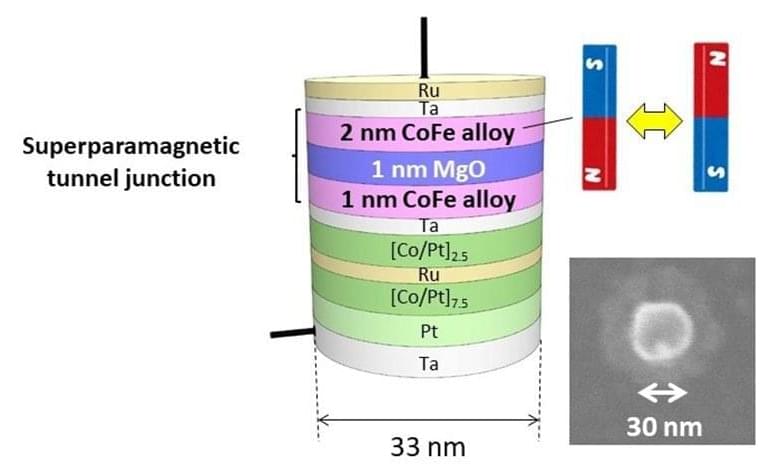
Tohoku University scientists in Japan have developed a mathematical description of what happens within tiny magnets as they fluctuate between states when an electric current and magnetic field are applied. Their findings, published in the journal Nature Communications, could act as the foundation for engineering more advanced computers that can quantify uncertainty while interpreting complex data.
Classical computers have gotten us this far, but there are some problems that they cannot address efficiently. Scientists have been working on addressing this by engineering computers that can utilize the laws of quantum physics to recognize patterns in complex problems. But these so-called quantum computers are still in their early stages of development and are extremely sensitive to their surroundings, requiring extremely low temperatures to function.
Now, scientists are looking at something different: a concept called probabilistic computing. This type of computer, which could function at room temperature, would be able to infer potential answers from complex input. A simplistic example of this type of problem would be to infer information about a person by looking at their purchasing behavior. Instead of the computer providing a single, discrete result, it picks out patterns and delivers a good guess of what the result might be.