Lifeboat Foundation

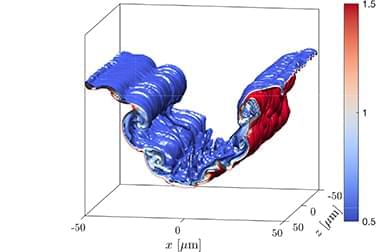
Simulating KH-, RT-, or RM-driven mixing using direct numerical simulations (DNS) can be prohibitively expensive because all the spatial and temporal scales have to be resolved, making approaches such as Reynolds-averaged Navier–Stokes (RANS) often the more favorable engineering option for applications like ICF. To this day, no DNS has been performed for ICF even on the largest supercomputers, as the resolution requirements are too stringent.⁸ However, RANS approaches also face their own challenges: RANS is based on the Reynolds decomposition of a flow where mean quantities are intended to represent an average over an ensemble of realizations, which is often replaced by a spatial average due to the scarcity of ensemble datasets. Replacing ensemble averages by space averages may be appropriate for flows that are in homogenous-, isotropic-, and fully developed turbulent states in which spatial, temporal, and ensemble averaging are often equivalent. However, most HED hydrodynamic experiments involve transitional periods in which the flow is neither homogeneous nor isotropic nor fully developed but may contain large-scale unsteady dynamics; thus, the equivalency of averaging can no longer be assumed. Yet, RANS models often still require to be initialized in such states of turbulence, and knowing how and when to initialize them in a transitional state is, therefore, challenging and is still poorly understood.

The goal of this paper is to develop a strategy allowing the initialization of a RANS model to describe an unsteady transitional RM-induced flow. We seek to examine how ensemble-averaged quantities evolve during the transition to turbulence based on some of the first ensemble experiments repeated under HED conditions. Our strategy involves using 3D high-resolution implicit large eddy simulations (ILES) to supplement the experiments and both initialize and validate the RANS model. We use the Besnard–Harlow–Rauenzahn (BHR) model,^9–12 specifically designed to predict variable-density turbulent physics involved in flows like RM. Previous studies have considered different ways of initializing the BHR model.