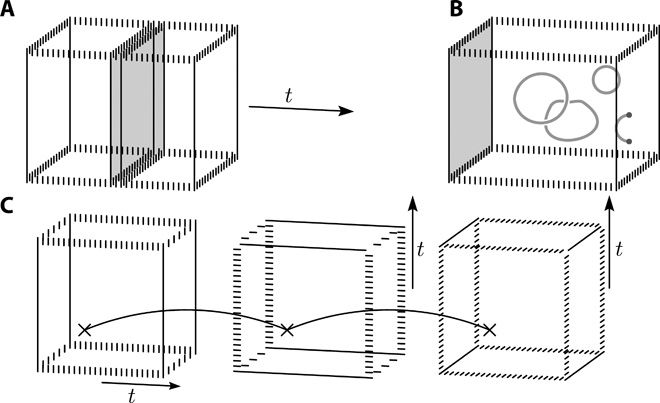
Fault-tolerant logic gates will consume a large proportion of the resources of a two-dimensional quantum computing architecture. Here we show how to perform a fault-tolerant non-Clifford gate with the surface code; a quantum error-correcting code now under intensive development. This alleviates the need for distillation or higher-dimensional components to complete a universal gate set. The operation uses both local transversal gates and code deformations over a time that scales with the size of the qubit array. An important component of the gate is a just-in-time decoder. These decoding algorithms allow us to draw upon the advantages of three-dimensional models using only a two-dimensional array of live qubits. Our gate is completed using parity checks of weight no greater than four. We therefore expect it to be amenable with near-future technology. As the gate circumvents the need for magic-state distillation, it may reduce the resource overhead of surface-code quantum computation considerably.
A scalable quantum computer is expected to solve difficult problems that are intractable with classical technology. Scaling such a machine to a useful size will necessarily require fault-tolerant components that protect quantum information as the data is processed (1–4). If we are to see the realization of a quantum computer, its design must respect the constraints of the quantum architecture that can be prepared in the laboratory. In many cases, for instance, superconducting qubits (5–7), this restricts us to two-dimensional architectures.
Leading candidate models for fault-tolerant quantum computation are based on the surface code (3, 8) due to its high threshold (9) and multitude of ways of performing Clifford gates (10). Universal quantum computation is possible if this gate set is supplemented by a non-Clifford gate. Among the most feasible approaches to realize a non-Clifford gate is by the use of magic-state distillation (11). However, this is somewhat prohibitive as a large fraction of the resources of a quantum computer will be expended by these protocols (12, 13).