Forget Netflix and binge watch these awesome farm-bot videos.
Get the latest international news and world events from around the world.

Privacy campaigner flags concerns about Microsoft’s creepy Productivity Score
It seems not everyone is happy about Microsoft’s productivity measuring tool. 😃
Watching, always watching.

Can lab-grown meat replace the real one?
A video on lab grown meat. Meat grown from cells taken from animals. 😃
How do you like your beef, the traditional way or 3D-printed? 🍖 🤔
Find out more at https://bit.ly/39kIeCN # engineering.
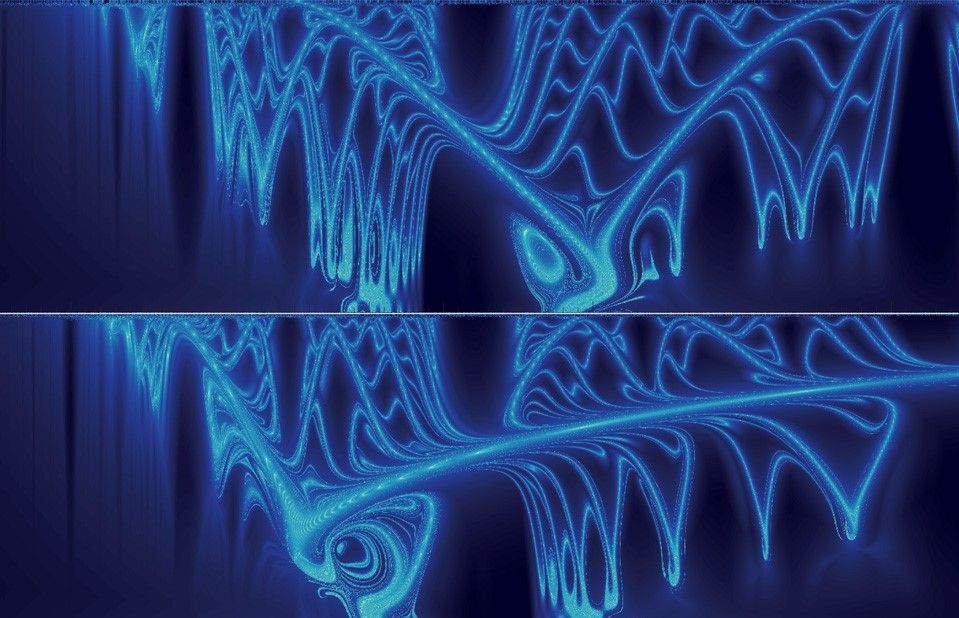
Arches of chaos in the solar system, luxury watch has bits of Stephen Hawking’s desk
Excerpts from the Red Folder.
If we had a “Physics paper title of the year award”, the 2020 winner would surely have to be “The arches of chaos in the solar system”, which was published this week in Science Advances by Nataša Todorović, Di Wu and Aaron Rosengren. In their paper, the trio “reveal a notable and hitherto undetected ornamental structure of manifolds, connected in a series of arches that spread from the asteroid belt to Uranus and beyond”. These manifolds are structures that arise from the gravitational interactions between the Sun and planets. They play an important role in spacecraft navigation and also explain the erratic nature of comets.
The paper is beautifully written, describing the manifolds as “a true celestial autobahn,” and going on to say that they “enable ‘Le Petit Prince’ grand tour of the solar system”. And if that has not piqued your curiosity, the figures are wonderful as well – with the above image being “Jovian-minimum-distance maps for the Greek and Trojan orbital configurations”.
The luxury watchmaker Bremont has released the Hawking Limited Edition watch that contains bits of a wooden desk once used by the late Stephen Hawking. The “exquisite chromometer” also contains pieces of a meteorite and is etched with a view of the night sky as seen from Oxford on 8 January 1942, Hawking’s place and date of birth. What is more, the serial number of the watch is printed on paper from a 1979 paper by Hawking that was cowritten by Gary Gibbons.
Gut microbes: The key to normal sleep
With fall and winter holidays coming up, many will be pondering the relationship between food and sleep. Researchers led by Professor Masashi Yanagisawa at the University of Tsukuba in Japan hope they can focus people on the important middlemen in the equation: bacterial microbes in the gut. Their detailed study in mice revealed the extent to which bacteria can change the environment and contents of the intestines, which ultimately impacts behaviors like sleep.
The experiment itself was fairly simple. The researchers gave a group of mice a powerful cocktail of antibiotics for four weeks, which depleted them of intestinal microorganisms. Then, they compared intestinal contents between these mice and control mice who had the same diet. Digestion breaks food down into bits and pieces called metabolites. The research team found significant differences between metabolites in the microbiota-depleted mice and the control mice. As Professor Yanagisawa explains, “we found more than 200 metabolite differences between mouse groups. About 60 normal metabolites were missing in the microbiota-depleted mice, and the others differed in the amount, some more and some less than in the control mice.”
The team next set out to determine what these metabolites normally do. Using metabolome set enrichment analysis, they found that the biological pathways most affected by the antibiotic treatment were those involved in making neurotransmitters, the molecules that cells in the brain use to communicate with each other. For example, the tryptophan–serotonin pathway was almost totally shut down; the microbiota-depleted mice had more tryptophan than controls, but almost zero serotonin. This shows that without important gut microbes, the mice could not make any serotonin from the tryptophan they were eating. The team also found that the mice were deficient in vitamin B6 metabolites, which accelerate production of the neurotransmitters serotonin and dopamine.

Electronic skin has a strong future stretching ahead
A material that mimics human skin in strength, stretchability and sensitivity could be used to collect biological data in real time. Electronic skin, or e-skin, may play an important role in next-generation prosthetics, personalized medicine, soft robotics and artificial intelligence.
“The ideal e-skin will mimic the many natural functions of human skin, such as sensing temperature and touch, accurately and in real time,” says KAUST postdoc Yichen Cai. However, making suitably flexible electronics that can perform such delicate tasks while also enduring the bumps and scrapes of everyday life is challenging, and each material involved must be carefully engineered.
Most e-skins are made by layering an active nanomaterial (the sensor) on a stretchy surface that attaches to human skin. However, the connection between these layers is often too weak, which reduces the durability and sensitivity of the material; alternatively, if it is too strong, flexibility becomes limited, making it more likely to crack and break the circuit.
David Sinclair — Aging Can Be Cured
Original Video ► https://www.youtube.com/watch?v=W_23474cHLg&ab_channel=RT
This channel will never be monetized.
Paypal ► https://goo.gl/ciSpg1
They say age breeds wisdom. But can we grow personally and mature, while staying young and healthy? Can ageing be cured just like any other disease? We asked David Sinclair, professor of genetics at Harvard Medical School.
David Andrew Sinclair is an Australian biologist and Professor of Genetics best known for his research on the biology of lifespan extension and driving research towards treating diseases of aging.
Sinclair is Co-Director of the Paul F. Glenn Laboratories for the Biological Mechanisms of Aging at Harvard Medical School. Sinclair obtained a Bachelors of Science (Honours Class I) at the University of New South Wales, Sydney, and received the Australian Commonwealth Prize. In 1995, he received a Ph.D. in Molecular Genetics then worked as a postdoctoral researcher at the Massachusetts Institute of Technology with Leonard Guarente. Since 1999 he has been a tenured professor in the Genetics Department of Harvard Medical School.
Sinclair has received over 25 awards including The Australian Commonwealth Prize, A Helen Hay Whitney Fellowship, the Nathan Shock Award, a Leukemia and Lymphoma Fellow, a MERIT Awards from the National Institutes of Health, the Merck Prize, the Arminese Fellowship, the Genzyme Outstanding Achievement in Biomedical Science Award, an Ellison Medical Senior Fellow, the Bio-Innovator award, the Bright Sparks Award for Top Scientists under 40, The Denham Harman Award in Biogerontology, a medal from the Australian Society for Medical Research, and a TIME 100 honoree, TIME magazine’s list of the 100 “most influential people in the world” (2014).
AI system finds, moves items in constricted regions
Artificial intelligence is being applied to virtually every aspect of our work and recreational lives. From determining calculations for the construction of towering skyscrapers to designing and building cruise ships the size of football fields, AI is increasingly playing a key role in the most massive projects.
But sometimes, all we want to do is move a can of beans.
According to a recently published abstract by researchers at the University of California, Berkeley, they have developed a mechanism that “couples a perception pipeline predicting a target object occupancy support distribution with a mechanical search policy that sequentially selects occluding objects to push to the side to reveal the target as efficiently as possible.”