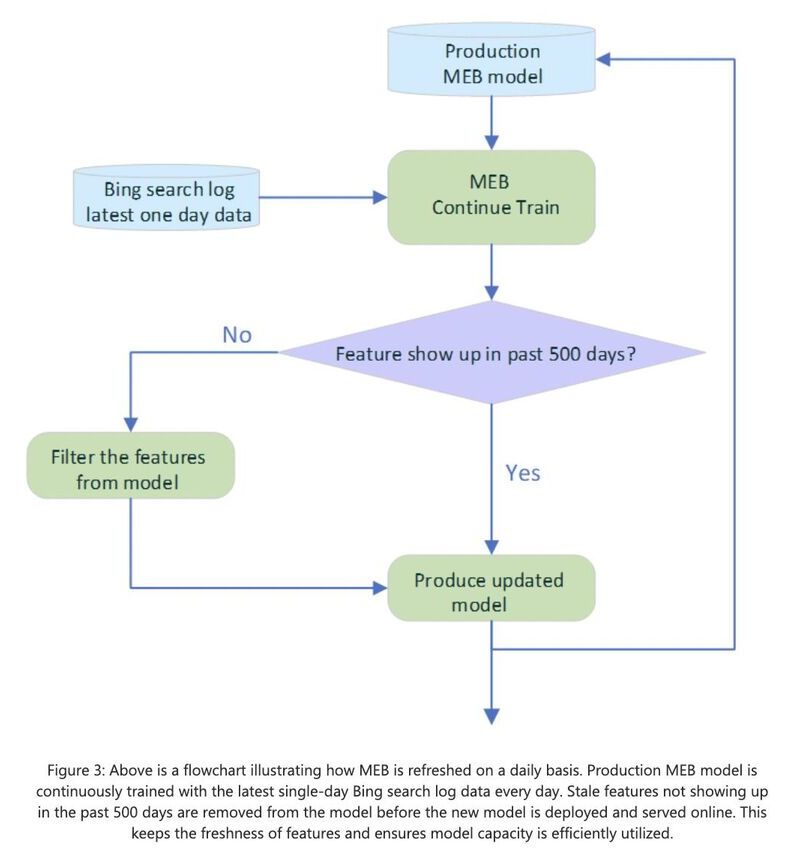
Drones are neat and fun and all that good stuff (I should probably add the caveat here that I’m obviously not referring to the big, terrible military variety), but when it comes to quadcopters, there’s always been the looming question of general usefulness. The consumer-facing variety are pretty much the exclusive realm of hobbyists and imaging.
We’ve seen a number of interesting applications for things like agricultural surveillance, real estate and the like, all of which are effectively extensions of that imaging capability. But a lot can be done with a camera and the right processing. One of the more interesting applications I’ve seen cropping up here and there is the warehouse drone — something perhaps a bit counterintuitive, as you likely (and understandably) associate drones with the outdoors.
Looking back, it seems we’ve actually had two separate warehouse drone companies compete in Disrupt Battlefield. There was IFM (Intelligent Flying Machines) in 2016 and Vtrus two years later. That’s really the tip of the iceberg for a big list of startups effectively pushing to bring drones to warehouses and factory floors.