Edible robots are here, and they might taste like gummy candy. Learn how these wiggly wonders could help in wildlife conservation.



This isn’t your normal wedding cake. The gummy bears on top can dance, their heads and arms moving thanks to injections of air through a pneumatic system, and the LED candles at the bottom are powered by batteries made out of chocolate. Such edible electronics have been proposed as a solution to electronic waste. The cake was unveiled at Expo 2025 in Osaka, Japan, on 13 April.
3Doodler, known for its 3D-printing pens, has announced a kid-friendly version of its Chef 3D pen that prints with candy instead of plastic filament. The new 3Doodler Candy, arriving later this year, swaps a power cord for a 45-minute rechargeable battery and uses gluten-free vegan isomalt capsules instead of sugar.
The candy comes out of the pen at 45 degrees Fahrenheit, so it’s safe for kids aged six and up to use.

New research shows that the magnetic part of light actively shapes how light interacts with matter, challenging a 180-year-old belief.
The team demonstrated that this magnetic component significantly contributes to the Faraday Effect, even accounting for up to 70% of the rotation in the infrared range. By proving that light can magnetically torque materials, the findings open unexpected pathways for advanced optical and magnetic technologies.
Revealing Light’s Hidden Magnetic Power
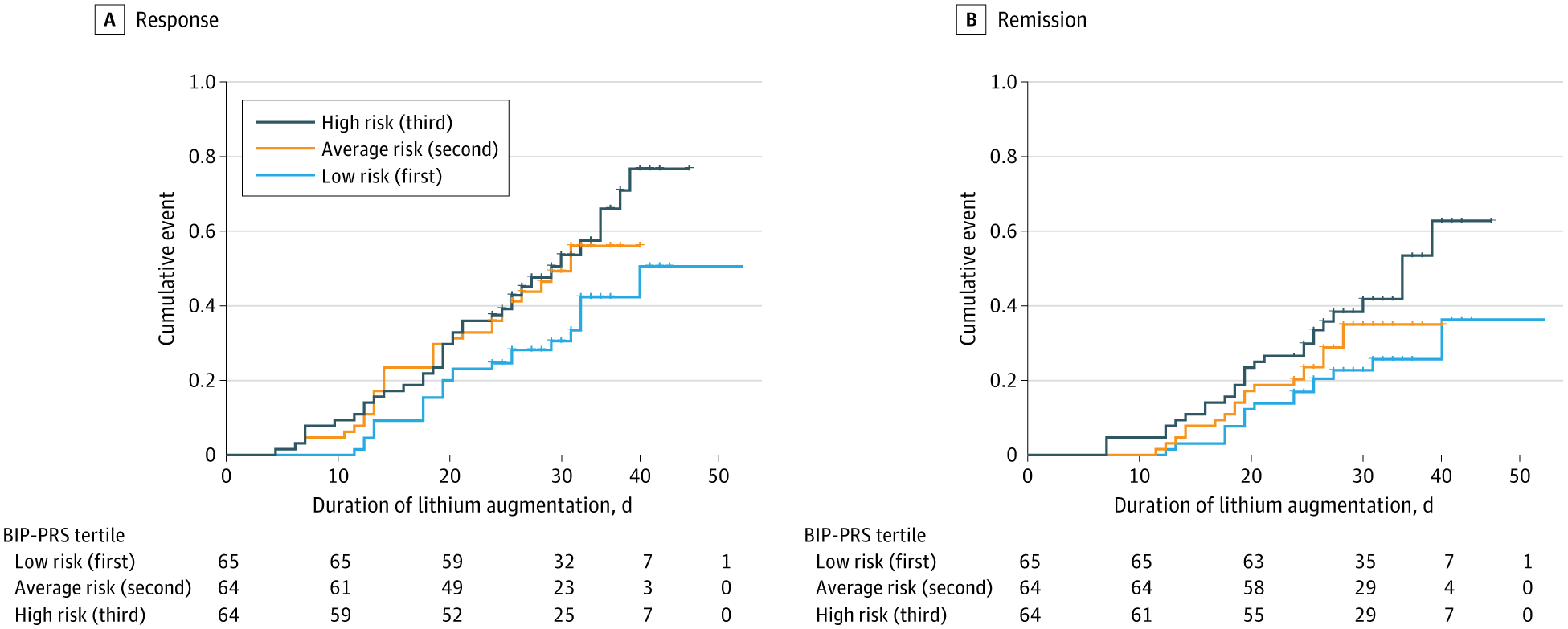
Higher polygenic risk scores for bipolar disorder were associated with favorable treatment outcomes after lithium augmentation in antidepressant non-responders with unipolar depression.
Question Are polygenic risk scores (PRS) for major psychiatric disorders associated with favorable treatment outcomes after lithium augmentation (LA) in major depression?
Findings In this cohort study with 193 patients with major depressive disorder (MDD) who did not respond to antidepressants, the PRS for bipolar disorder (BIP) was significantly associated with response and remission after at least 4 weeks of LA. Additionally, we found an association between the MDD-PRS and LA response.
Meaning Individuals with a higher polygenic burden for BIP and lower polygenic burden for MDD are more likely to experience favorable treatment outcomes following LA, offering new opportunities for personalized medicine approaches.
New research finds that dying cells leave a “footprint of death” that guides immune responses — but viruses like influenza can exploit this signaling. The discovery, published in Nature Communications, offers new insight into cell death, viral transmission, and potential drug targets.
New insights into the aftermath of cell death might ultimately inform drug development.
Necrosis Inhibitors To Pause The Diseases Of Aging — Dr. Carina Kern Ph.D. — CEO, LinkGevity
Dr. Carina Kern, Ph.D. is the CEO of LinkGevity (https://www.linkgevity.com/), an AI-powered biotech company driving innovation in drug discovery for aging and resilience loss.
Dr. Kern has developed a new Blueprint Theory of Aging, which takes an integrative approach to understanding aging, combining evolutionary theory, genetics, molecular mechanisms and medicine, and is used to structure LinkGevity’s AI.
Dr. Kern’s labs are based at the Babraham Research Campus, affiliated with the University of Cambridge and her research has led to the development of a first-in-class necrosis inhibitor targeting cellular degeneration (Anti-Necrotic™). This novel therapeutic is ready to begin Phase II clinical trials later this year, as a potential breakthrough treatment for aging, with UK Government, Francis Crick Institute KQ labs, and European Union (Horizon) support.
The Anti-Necrotic™ has also been selected as one of only 12 global innovations for NASA’s Space-Health program, recognizing its potential to mitigate accelerated aging in astronauts on long-duration space missions.

From the article:
Following a vegetarian diet can be a boon for your health, even possibly cutting your risk of certain chronic illnesses, according to the Mayo Clinic. Yet a recent study, conducted by nutrition experts and published in the Nature journal npj Aging, suggests that not everyone will experience the same benefits when they cut out meat entirely. Adults over the age of 60 may have different nutritional needs, meaning a more diverse diet could instead help them live longer… Utilizing data from the Chinese Longitudinal Healthy Longevity Survey, the study reviewed information from nearly 2,900 Chinese older adults who were considered to be healthy. Participants’ diets were categorized four ways:
- vegan (avoiding any animal products, including eggs, seafood, or dairy) — ovo-vegetarian (vegetarian plus the inclusion of eggs) — pesco-vegetarian (vegetarian plus the inclusion of fish and seafood) — omnivorous (eating both plant-and animal-based products)
After an average follow-up period of six years, “Individuals who maintained omnivorous diets from age 60 years had higher odds of achieving healthy aging” versus those who “consistently” followed vegetarian eating patterns. When the team further analyzed the health data of those who survived to age 80, omnivorous eaters were more likely than vegetarians to avoid major chronic disease, physical function impairment, and cognitive impairment.
“Given age-related physiological changes in digestive and metabolic systems” in aging adults, the study specifically flagged the potential for muscle loss and bone fracture for those adhering to vegetarian diets. Another interesting discovery: older adults following a vegan diet were “most strongly associated with adverse effects on healthy aging,” which the text attributes to an increased risk of protein deficiency.”
npj Aging — Vegetarian diet and healthy aging among Chinese older adults: a prospective study. npj Aging 11, 25 (2025). https://doi.org/10.1038/s41514-025-00213-4
