A structural phenomenon traditionally confined to inanimate systems has now been observed in biology.


A new symmetry-breaking scenario provides a comprehensive description of magnetic behavior associated with the anomalous Hall effect.
In 1879 Edwin Hall discovered that a flat conductor carrying current, when placed in a magnetic field, will develop a transverse voltage caused by the deflection of charge carriers. Two years later he discovered that the same effect arises in ferromagnets even without an applied magnetic field. Dubbed the anomalous Hall effect (AHE), that phenomenon, alongside the ordinary Hall effect, not only catalyzed the rise of semiconductor physics and solid-state electronics but also laid the groundwork for a revolutionary convergence of topology and condensed-matter physics a century after Hall’s discoveries. Recent experiments, however, have uncovered behavior that cannot be explained with current theories for the AHE.


European researchers are developing quantum computers using light and glass, in a collaboration that promises breakthroughs in computing power, battery technology and scientific discovery.
Giulia Acconcia grew up in the picturesque, historic town of Spoleto, nestled in the foothills of Italy’s Apennine Mountains. Already in secondary school, she became fascinated with modern technology—a passion that would shape her future.
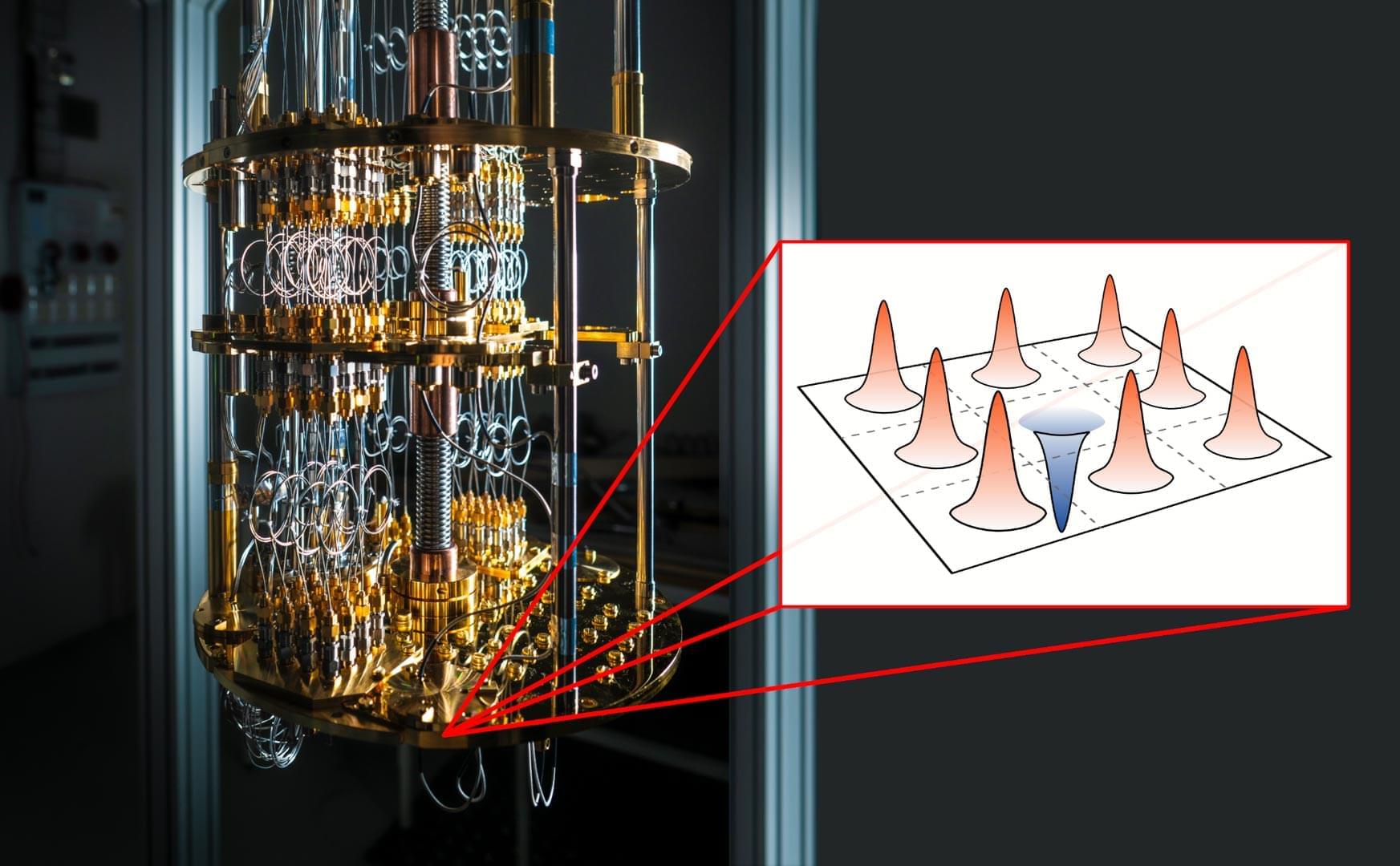
Her love of electronics led her to the Polytechnic University of Milan, Italy, where she now finds herself at the forefront of quantum computing research.
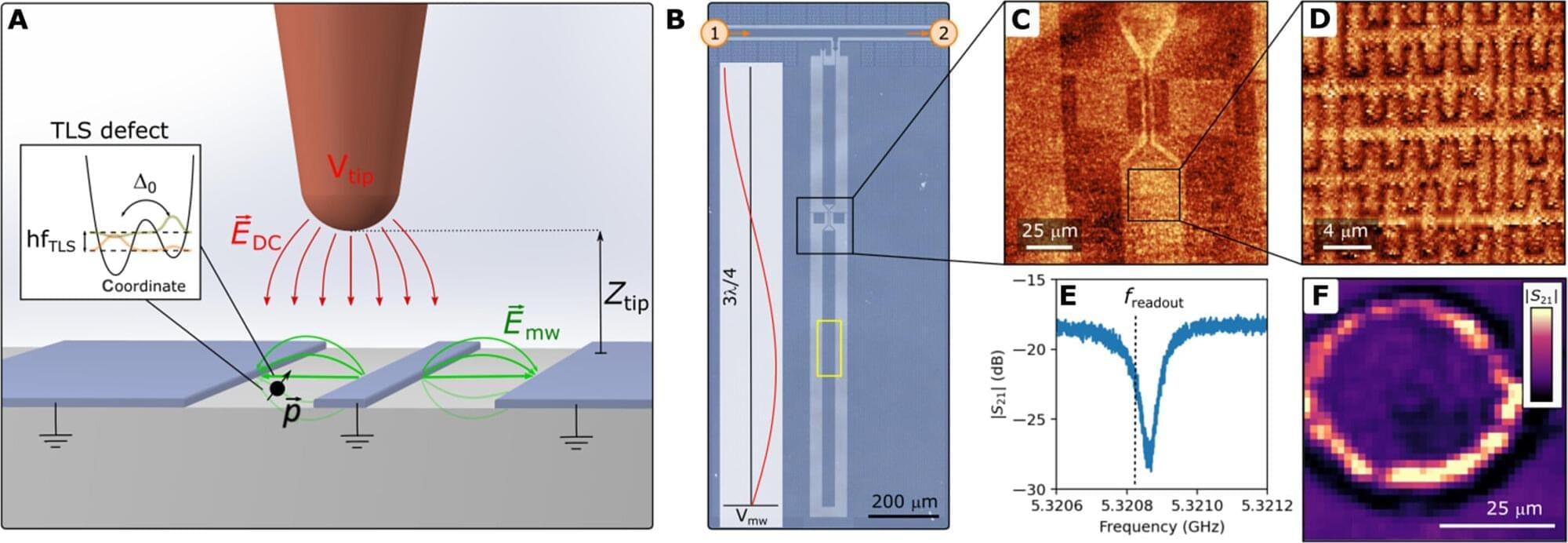
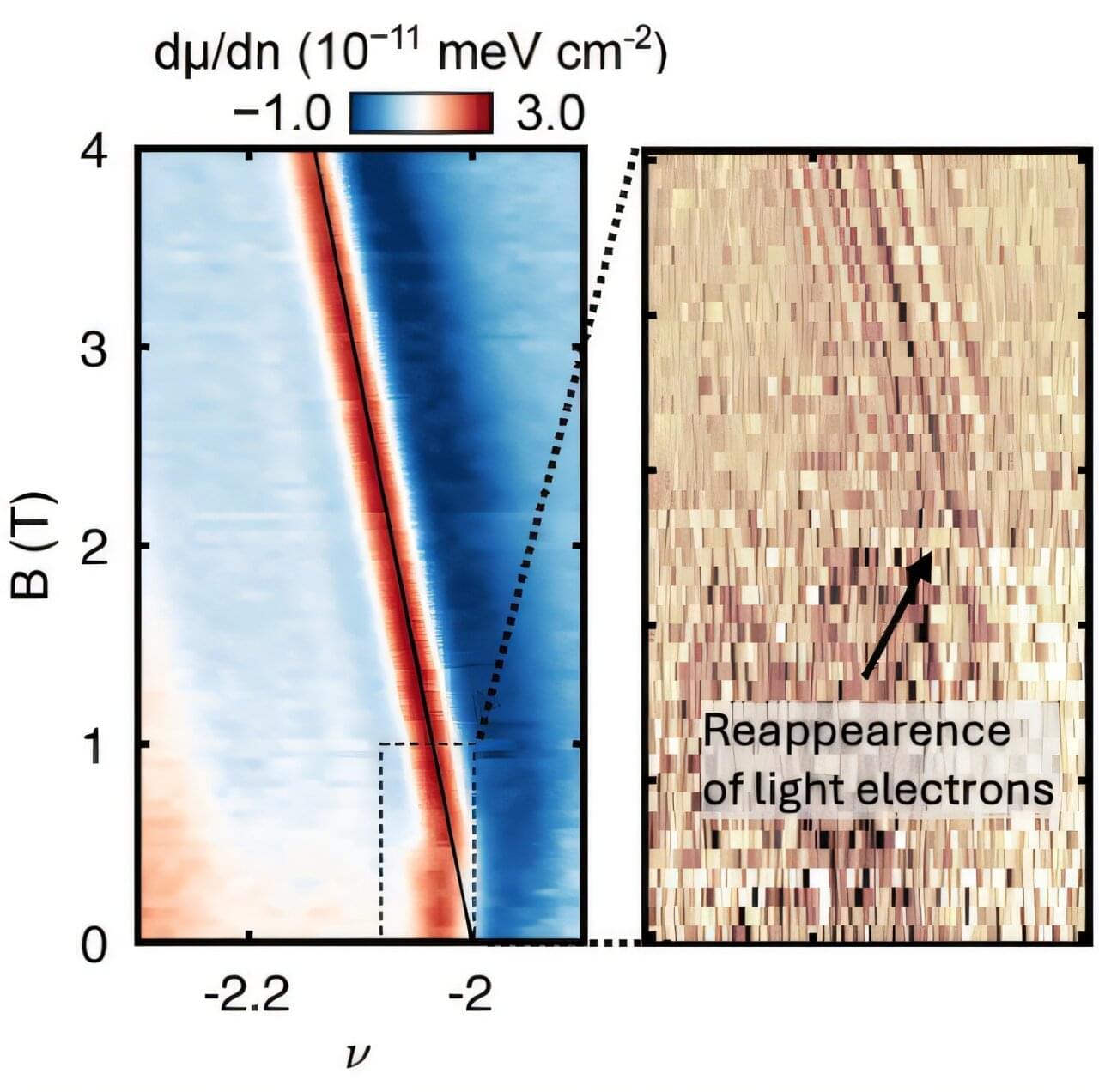
Electrons play many roles in solid materials. When they are weakly bound and able to travel—i.e., mobile—they can enable electrical conduction. When they are bound, or “heavy,” they can act as insulators. However, in certain solid materials, this behavior can be markedly different, raising questions about how these different types of electrons interact.
In a study just published in Nature Physics, researchers working with Professor of Physics and Applied Physics Amir Yacoby at Harvard examined the interplay between both types of electrons in this material, shedding new light on how they may help form novel quantum states.
“Before our work, people could only ask ‘What is the overall ground state?’” said Andrew T. Pierce, one of the paper’s lead authors. Pierce, currently a fellow at Cornell University, was a graduate student in Yacoby’s lab when they began to study this question. What wasn’t clear was the true nature of these different states and how the separate light and heavy electrons joined forces to form them.
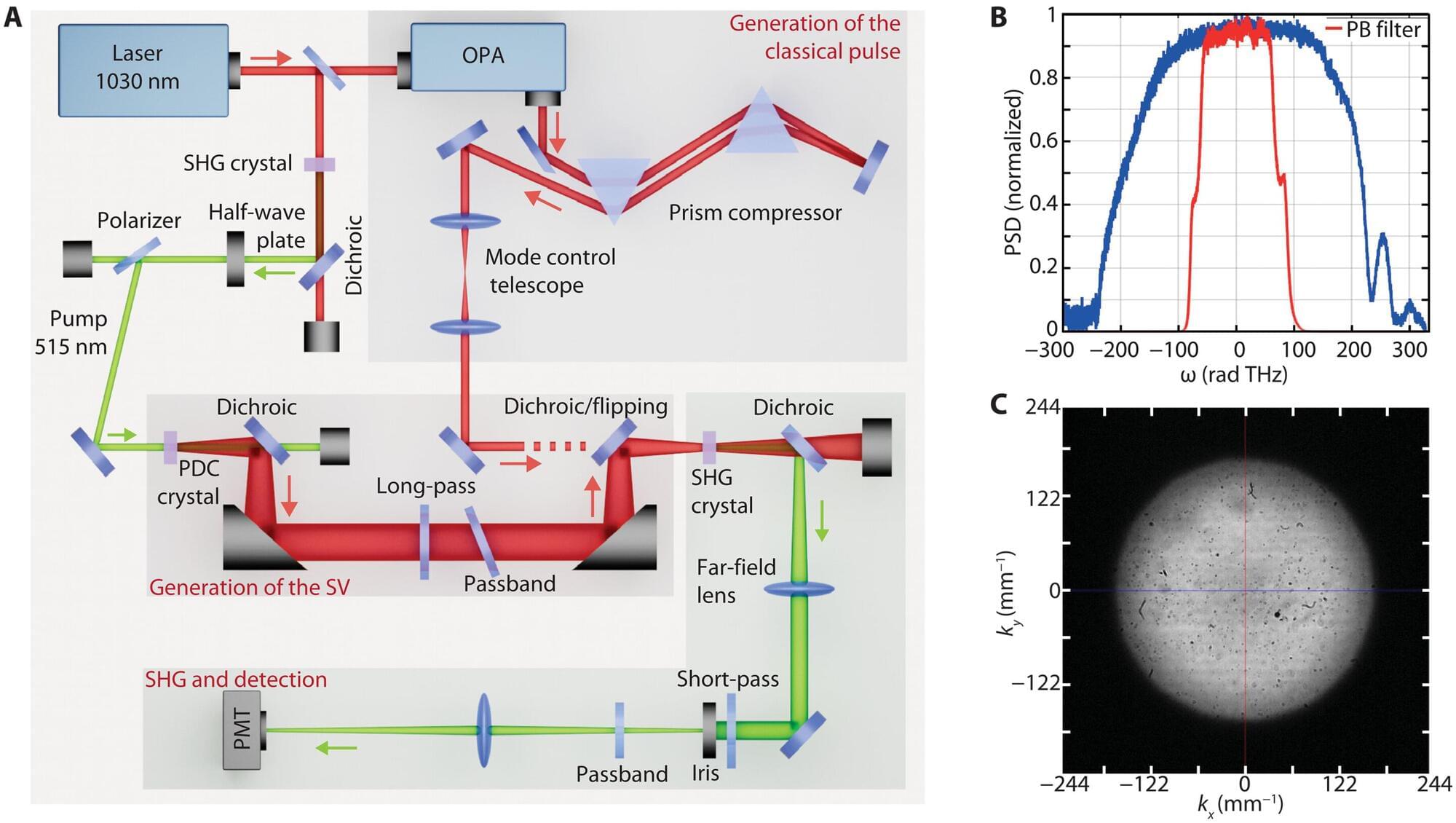
Technologies such as biomedical imaging and spectroscopy could be enhanced by a discovery in research that involved several institutions, including the University of Glasgow. Scientists have found that two-photon processes, which have applications in the study of Alzheimer’s disease and other nervous system disorders, can be strengthened by quantum light at far higher levels than previously thought possible.
The processes normally require high-intensity light but this can cause samples to be damaged or bleached.
It was suggested many years ago—and has since been demonstrated—that entangled photon pairs could overcome this limitation. However, it has been widely believed that this quantum enhancement only survives for very faint light, raising doubts about the usefulness of the approach.

Physicists confirm DT fusion insights from a 1938 experiment. The findings connect past theory with current fusion efforts. A team at Los Alamos National Laboratory has successfully recreated a significant yet largely overlooked physics experiment: the first recorded observation of deuterium-trit