Shared with Dropbox.



A speech prosthetic developed by a collaborative team of Duke neuroscientists, neurosurgeons, and engineers can translate a person’s brain signals into what they’re trying to say.

In a groundbreaking feat, a deep space experiment travelling on NASA’s Psyche spacecraft has successfully transmitted data via a near-infrared laser to Earth from 16 million kilometres away!
A deep space experiment traveling on NASA’s Psyche spacecraft has just beamed a message via laser to Earth from far beyond the Moon for the first time, an achievement that could transform how spacecraft communicate.
In the farthest-ever demonstration of this type of optical communication, the Deep Space Optical Communications (DSOC) beamed a near-infrared laser encoded with test data from its position around 16 million kilometers (10 million miles) away – which is around 40 times farther than the Moon is from Earth – to the Hale Telescope at Caltech’s Palomar Observatory in California.
The DSOC is a two-year tech demonstration riding along on Psyche as it makes its way to its prime target, asteroid Psyche. The demo achieved “first light” on November 14, according to NASA’s Jet Propulsion Laboratory (JPL), which manages both missions, thanks to an incredibly precise maneuver that saw its laser transceiver lock onto JPL’s powerful uplink laser beacon at its Table Mountain Observatory, which allowed the DSOC’s transceiver to aim its downlink laser at Caltech’s observatory 130 kilometers (100 miles) away.

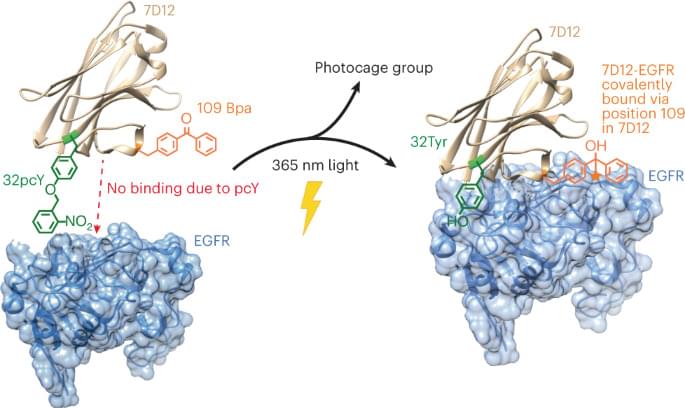
New light activated cancer treatment.
Several antibodies and antibody fragments have been previously developed for the treatment of various diseases, including cancer3,4. These antibodies bind to cell surface receptors expressed at higher levels on cancer cells, addressing a major challenge of selective cell targeting in cancer therapy. Although full-length antibodies have shown promise for treatment of several cancers, limited success has been demonstrated in eliminating solid tumors. Due to their large size, full-length antibodies are unable to diffuse deep into solid tumors5. In addition, it has been shown that high-affinity antibodies bind to the periphery of the tumor tissues, forming a barrier and preventing their further penetration6. Some studies in patients with cancer estimate that only 0.01% of the injected antibodies accumulate per gram of solid tumor tissue7. Small antibody fragments with low molecular weight can diffuse much deeper into tissues, presenting an excellent alternative to full-length antibodies. However, small antibody fragments have a low residence time in the body and often have a higher rate of dissociation (koff) from the target compared with full-length antibodies, limiting their clinical utility8. To address these challenges, antibody fragments are often multimerized9,10 and/or conjugated to larger proteins11, which increases the size of antibody fragments, again reducing their ability to penetrate into the tumor.
One solution to overcome the limitation of low residence time would be to replace the noncovalent interactions between the antibody fragment and its antigen with a covalent bond. In a notable effort, an affibody containing a photocrosslinker in its antigen binding region was shown to covalently link to its antigen and demonstrated higher accumulation on tumor tissues12. Another pioneering study involved developing affibodies containing a latent bioreactive amino acid in their antigen binding region that forms a covalent bond with the target antigen by proximity-dependent reaction without any external impetus13. However, the former had substantially lower binding affinity compared with its wild-type (wt) counterpart and thus, requires using a high concentration for efficient initial binding, while the latter could react with target antigen expressed on healthy cells causing side effects.
Although antibody-based therapeutics are more selective than several cytotoxic small molecule drugs used for cancer treatment, they can cause cardiac toxicity and skin reactions14. These side effects are due to the binding of the antibody to its receptor antigen expressed on healthy cells. This challenge could be addressed by activating antibody–antigen binding in the tumor microenvironment. One notable example in this direction is the development of antibodies containing an inhibitory N-terminal domain that is removed by tumor-specific proteases15. However, this approach would be difficult to extend to antibody fragments whose N terminus is not involved in antigen binding. We and others have also developed light-activated antibody fragments either by site-specific installation of photocaged functional groups or by introducing light-responsive proteins into antibodies16,17,18. In principle, such antibodies could be activated at the site of tumors using surgically implanted biocompatible light-emitting diodes (LEDs)19, thereby reducing the side effects of antibody-based therapeutics.
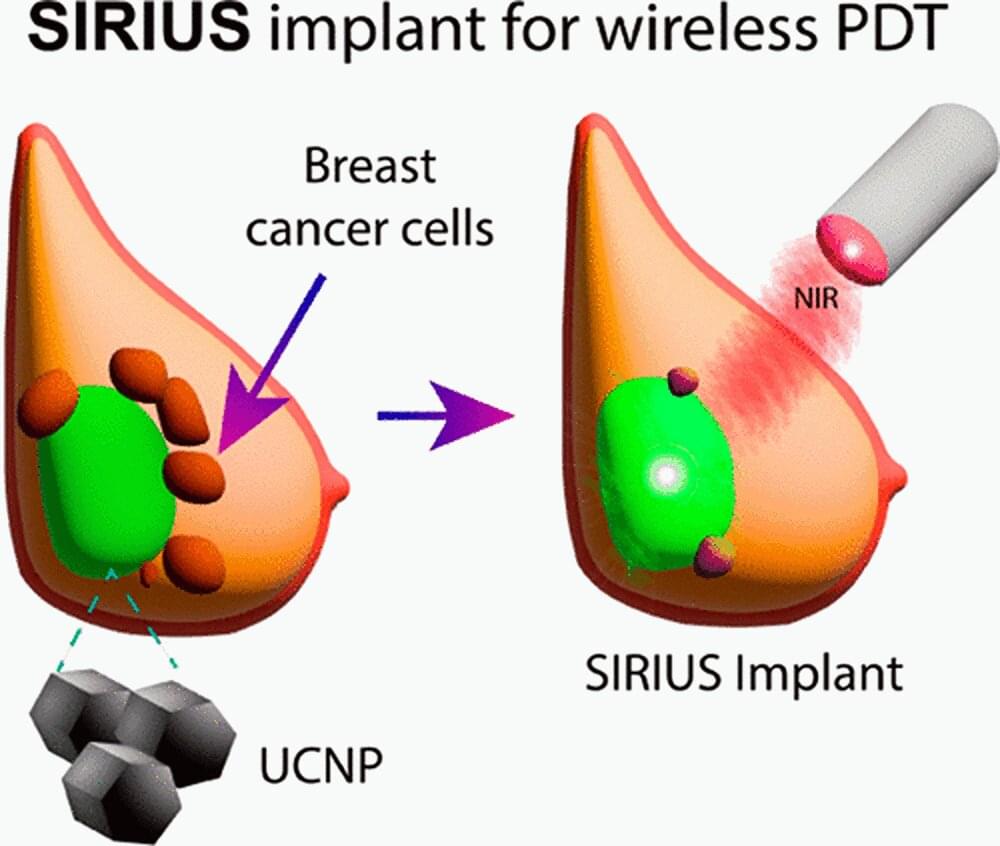
This is a nontoxic version of cancer treatment that works on any type of cancer.
Breast cancer is the most common cancer affecting women in Singapore. Treatment is multimodal and often involves surgery to remove the cancer and lymph nodes involved.
Adjuvant therapy, given after the initial treatment, is used to irradiate and destroy micrometastases, which are cancer cells in the blood stream or lymphatics, to decrease recurrence. This form of therapy is subdivided into local (radiotherapy) and systemic therapy (endocrine therapy, chemotherapy and targeted therapy).
Studies have shown that patient satisfaction has increased with breast conserving therapy (BCT) where only the tumor and a margin is removed from the body post mastectomy, compared to full mastectomy alone, which removes all parts of the breast. For BCT, radiotherapy has to be administered after lumpectomy, which removes other abnormal tissue from the breast and some normal tissue around it.
Move over Perseverance, a new kind of robot is coming to town.
Starship Troopers.
by Robert A. Heinlein.
Read by Christopher Hurt.
Originally issued by NLS on cassette in 1982
Can we refrain from inane comments about fascism? Unless you have something constructive to say I’ll probably just delete it and block you from commenting in the future. Or I might turn off comments altogether. With that out of the way, enjoy the book.
“Thousands of years in the future, a young man joins mobile infantry and fights in an interplanetary war against insect-like aliens.“
Chapter list:
00:00:00 — (i) Book info.
00:01:03 — (01)
00:38:44 — (02)
01:17:03 — (03)
01:35:28 — (04)
01:51:35 — (05)
02:24:49 — (06)
03:03:54 — (07)
03:23:54 — (08)
03:49:49 — (09)
04:05:24 — (10)
04:36:24 — (11)
05:13:19 — (12)
06:25:44 — (13)
08:20:23 — (14)
Like these books? Want to help?
These books come from the National Library Services.
I encourage you to donate:
https://www.loc.gov/nls/about/donate/
Year 2015 face_with_colon_three
A brain-computer interface lets a quadriplegic woman pilot an F-35 flight simulator with the power of her mind alone.
Join us on Patreon! https://www.patreon.com/MichaelLustgartenPhD
Discount Links:
Epigenetic, Telomere Testing: https://trudiagnostic.com/?irclickid=U-s3Ii2r7xyIU-LSYLyQdQ6…M0&irgwc=1
Use Code: CONQUERAGING
NAD+ Quantification: https://www.jinfiniti.com/product/intracellular-nad-test/
Use Code: ConquerAging At Checkout.
Oral Microbiome: https://www.bristlehealth.com/?ref=michaellustgarten.
Enter Code: ConquerAging.
At-Home Metabolomics: https://www.iollo.com?ref=michael-lustgarten.
Use Code: CONQUERAGING At Checkout.
At-Home Blood Testing (SiPhox Health): https://getquantify.io/mlustgarten.