Development of a prognostic model for poststroke dementia using multiple international cohorts: a STROKOG collaboration study.
Background and Objectives.
Get the latest international news and world events from around the world.
Widespread liver dysfunction in Down syndrome
Patients with detectable virus-specific T cells before checkpoint inhibitor therapy in PML demonstrated better survival rates and functional recovery than those without.
Question Are pretreatment JC virus-and/or BK virus-specific T cells in the blood associated with the efficacy of immune checkpoint inhibitors (ICIs) in progressive multifocal leukoencephalopathy (PML)?
Findings In this cohort study of 111 patients with PML treated with ICIs, those with detectable virus-specific T cells (n = 21) had significantly higher response rates and longer survival than both T cell–negative patients (n = 22) and those with unknown status (n = 68).
Carotid Artery Stenosis—Impactful Bias in Ischemic Stroke Classification
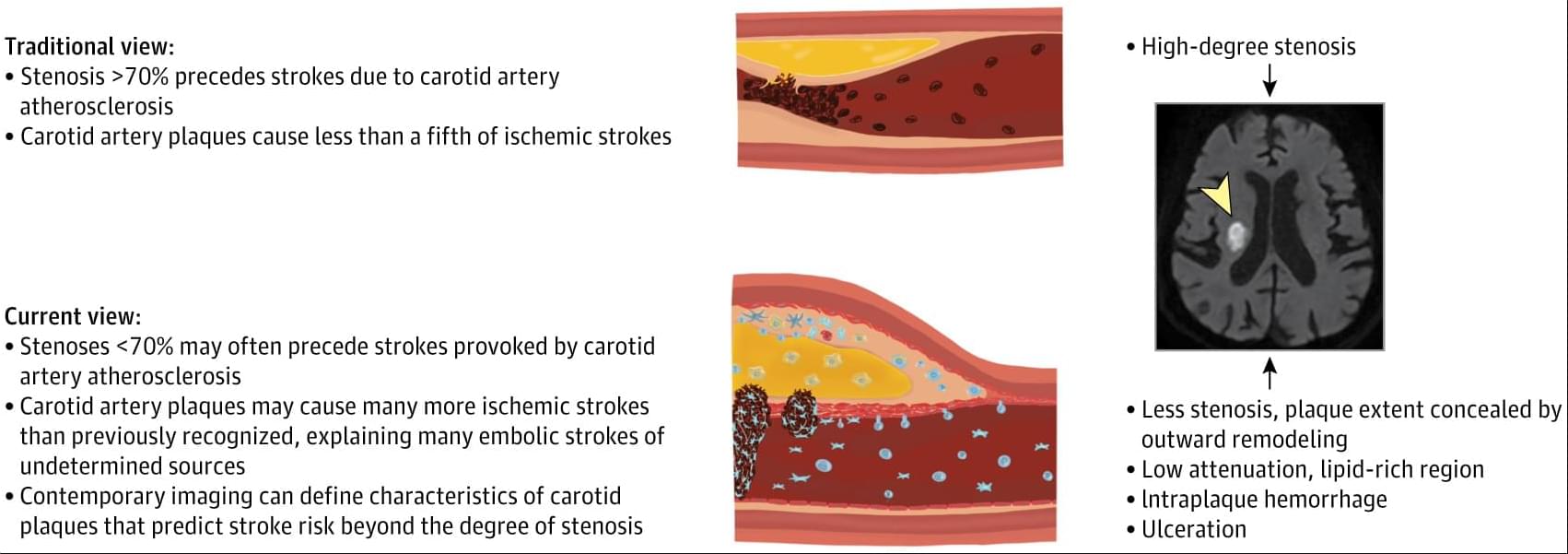
💬 Editorial: Stroke risk classification that relies solely on carotid stenosis severity overlooks patients with nonobstructive but high-risk carotid plaques, underestimating the true contribution of carotid disease to ischemic stroke.
Recent European Society of Cardiology guidelines and Carotid Plaque–RADS offer improved risk stratification by accounting for plaque features, with evidence showing significant gains in predictive accuracy.
This Viewpoint argues that risk classification in ischemic stroke should be expanded beyond stenosis severity to encompass other complementary features, such as plaque morphology, composition, and inflammation.
Stress-reduction molecule has potential to treat aging and metabolic disorders
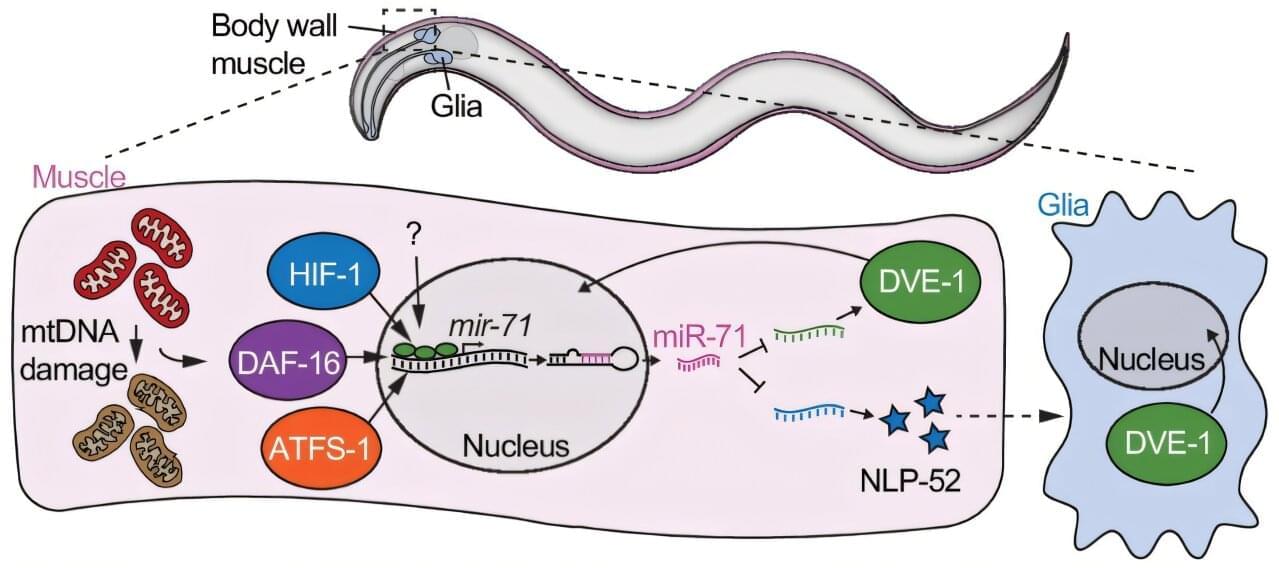
University of Queensland researchers say the discovery of a new stress reduction role for a naturally occurring molecule in the body could lead to new drugs and treatment for metabolic disorders and aging.
Professor Steven Zuryn, a molecular geneticist from UQ’s Queensland Brain Institute, was part of a team that found that very small RNA molecules, called microRNAs, bind to genes and prevent them from being over-activated.
MicroRNAs were discovered in C. elegans about 30 years ago and have since been shown to be important in human health and disease. This initial discovery led to the 2024 Nobel Prize in Physiology or Medicine.
Hot, Black Ice Might Be Responsible For Neptune’s Wild Magnetism
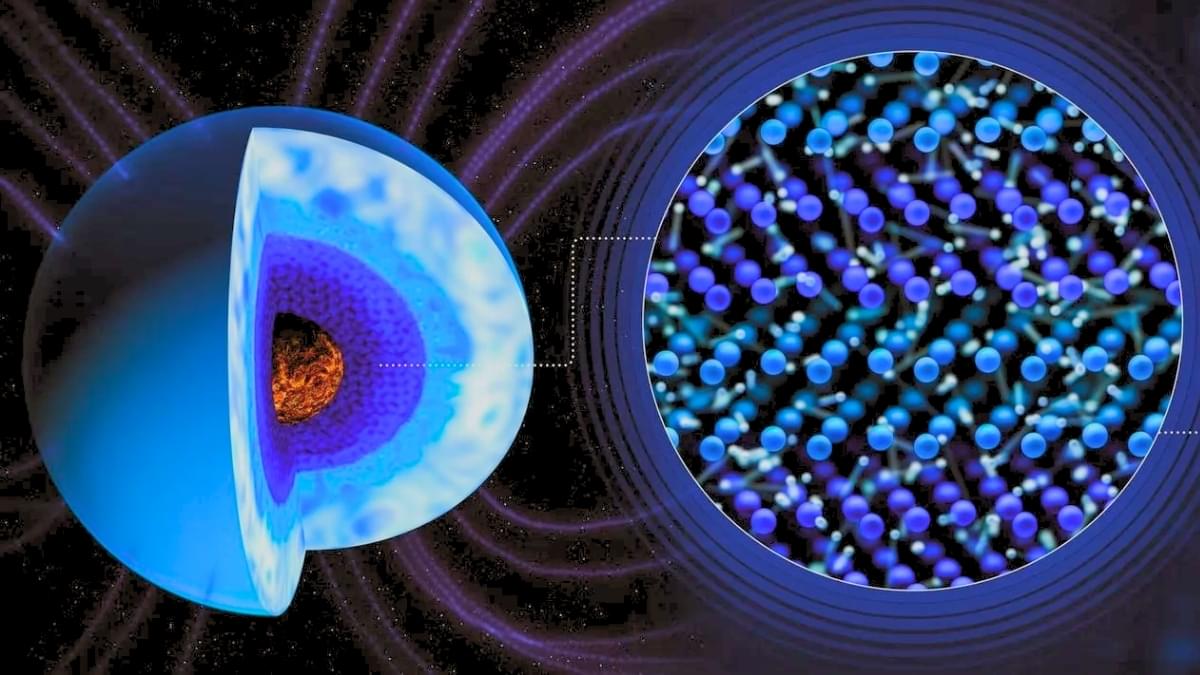
Inside the cores of ice giant planets, the pressure and temperature are so extreme that the water residing there transitions into a phase completely unfamiliar under natural conditions on Earth.
Known as ‘superionic water’, this form of water is a type of ice. However, unlike regular ice, it’s actually hot, and also black.
For decades, scientists thought that the superionic water in the core of Neptune and Uranus was responsible for the wild, unaligned magnetic fields that the Voyager 2 spacecraft saw when passing them.
Visceral Fat Removal Extends Lifespan: Who Has The Lowest?
Join us on Patreon! https://www.patreon.com/MichaelLustgartenPhD
Discount Links/Affiliates:
Blood testing (where I get the majority of my labs): https://www.ultalabtests.com/partners/michaellustgarten.
Blood testing with LifeExtension.com: https://www.anrdoezrs.net/click-101614996-15750394
At-Home Metabolomics: https://www.iollo.com?ref=michael-lustgarten.
Use Code: CONQUERAGING At Checkout.
Clearly Filtered Water Filter: https://get.aspr.app/SHoPY
Epigenetic, Telomere Testing: https://trudiagnostic.com/?irclickid=U-s3Ii2r7xyIU-LSYLyQdQ6…M0&irgwc=1
Human-Centric Intelligence: A New Paradigm For AI Decision Making
In my latest Forbes article, I explore one of the most critical questions facing leaders today:
How do we use AI to augment human intelligence rather than diminish it?
AI’s true power isn’t about automation alone—it’s about amplifying human judgment, creativity, and decision-making.
#AI #HumanCentricAI #artificialintelligence #tech #AugmentedIntelligence #Forbes #Leadership #Cybersecurity #EmergingTechnology #DigitalTransformation
Human-centric AI is the new frontier; it is not AI against human intelligence, but AI with human intelligence.