A vital ocean current in the tropics suddenly stopped for the first time in decades, leaving scientists stunned. What unfolded off the coast of Panama in early 2025 could signal something far more disruptive than anyone anticipated.



In controlled experiments, engineers have shown that electricity can be transmitted through the air using highly controlled electromagnetic fields and resonant coupling techniques, conceptually similar to the way data is sent via Wi-Fi but tailored for energy transfer.
These approaches build on decades of research into magnetic resonance and inductive power transfer, which seek to send energy efficiently across short distances without physical contact between transmitter and receiver…
…Past research from the university demonstrated that magnetic loop antennas can transfer power wirelessly at relatively high efficiency over short ranges, offering insights into how to optimize coupling and reduce energy losses.
More recent demonstrations reported in global tech news describe Finnish teams successfully powering small devices through the air using wireless power transfer methods.
Finland continues to make progress in the field of wireless electricity transmission, an area of research that aims to send power through the air without the use of traditional cables or plugs.
Recent demonstrations and experiments by Finnish researchers have highlighted steady advancements in technology that could one day reshape how devices are powered, though widespread commercial deployment remains distant.

The potential use of psychedelics in the treatment of various mental health conditions has made these drugs a hot area of scientific research, as well as growing public interest. A variant of ketamine called esketamine is already FDA approved and utilized for treatment-resistant depression, and the FDA has designated formulations of psilocybin and MDMA for the treatment of depression and PTSD, respectively, as “breakthrough therapies,” a process designed to expedite their development and review. NIDA is actively funding research on these compounds—NIDA and the National Institute on Mental Health are the largest funders of psychedelic research at NIH—as they represent a potential paradigm shift in the way we address substance use disorders too. Yet there is much we still do not know about these drugs, the way they work, and how to administer them, and there is danger of the hype getting out ahead of the science.
The promise of psychedelic compounds likely centers on their ability to promote rapid neural rewiring.1 Recent preclinical studies have suggested that the “neuroplastogen” properties of psilocybin, for example, may have to do with its ability to bind to 5HT2A (serotonin) receptors inside neurons, something that serotonin itself cannot do.2 That rewiring may explain these compounds’ relatively long-lasting effects, even with just one or a few administrations. Some trials have found effects lasting weeks3, but smaller studies (and anecdotes) are suggestive of much longer durations. What is needed is sound scientific research including clinical trials that can substantiate therapeutic efficacy, duration, and safety in large numbers of participants.
As part of a research study, psychedelics are administered by clinicians within highly controlled settings. This is important not only for safety reasons but because contextual factors and expectations play a crucial role in their effectiveness.4 Whether a patient has a positive or negative experience depends to a significant extent upon their mindset going into the experience and whether the setting is one in which they feel secure. This raises an important question—the extent (if any) to which the clinician’s time and attention and/or therapeutic approach play a role in psychedelics’ therapeutic efficacy—where much more research is needed. The extent to which psychotherapy is necessary in conjunction with psychedelics and which methods work best is an open question.
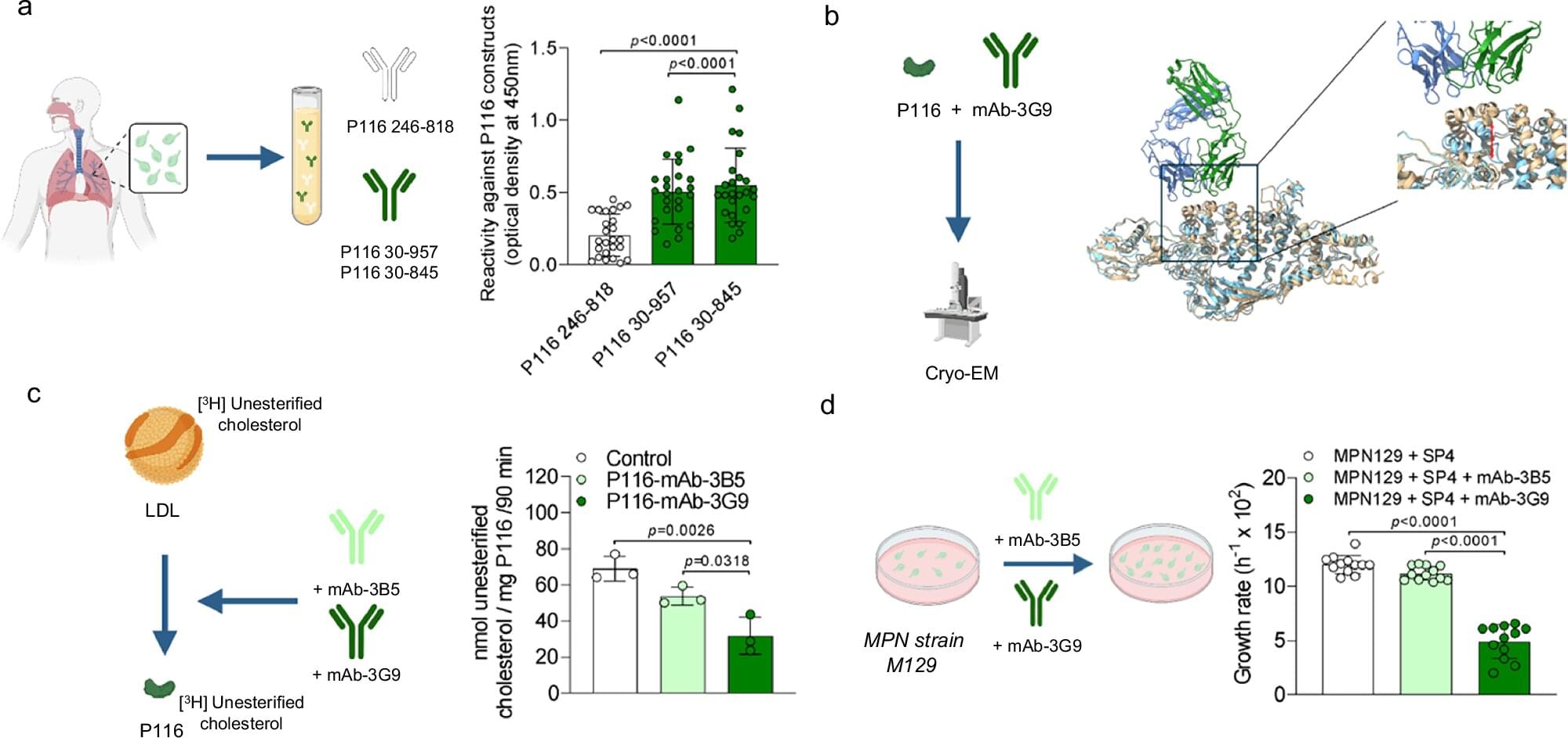
A multidisciplinary team has uncovered a key mechanism that allows the human bacterium Mycoplasma pneumoniae—responsible for atypical pneumonia and other respiratory infections—to obtain cholesterol and other essential lipids directly from the human body.
The discovery, published in Nature Communications, was co-led by Dr. Noemí Rotllan, from the Sant Pau Research Institute (IR Sant Pau) and the Center for Biomedical Research in Diabetes and Associated Metabolic Disorders (CIBERDEM); Dr. Marina Marcos, from the Autonomous University of Barcelona (UAB); and Dr. David Vizarraga, from the Institute of Molecular Biology of Barcelona of the Spanish National Research Council (IBMB-CSIC) and the Center for Genomic Regulation (CRG).
Overall coordination was led by Dr. Joan Carles Escolà-Gil, from IR Sant Pau and CIBERDEM; Dr. Jaume Piñol, from UAB; and Dr. Ignacio Fita, from IBMB-CSIC. The study also involved collaboration from the Institute of Biotechnology and Biomedicine of the UAB (IBB-UAB), the Center for Biomedical Research in Cardiovascular Diseases (CIBERCV), and other leading institutions.
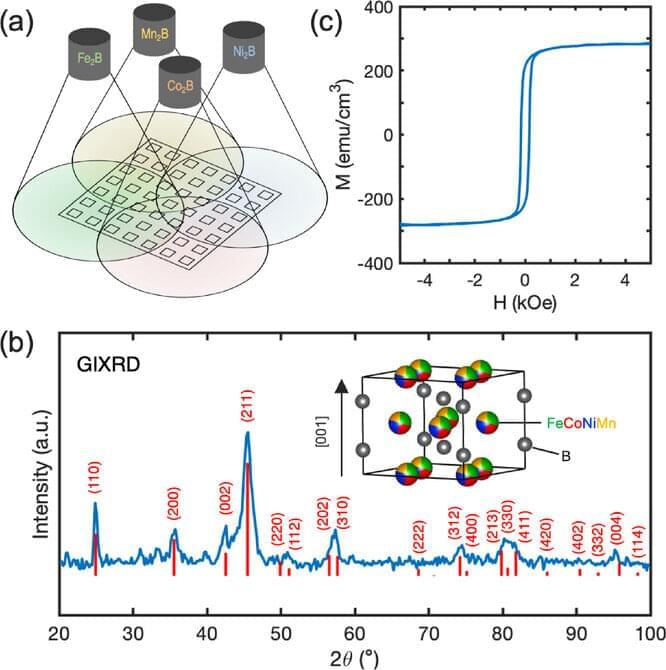
Georgetown University researchers have discovered a new class of strong magnets that do not rely on rare-earth or precious metals—a breakthrough that could significantly advance clean energy technologies and consumer electronics such as motors, robotics, MRI machines, data storage and smart phones.
A key figure of merit for a magnet is the ability of its magnetization to strongly prefer a specific direction, known as magnetic anisotropy, which is a cornerstone property for modern magnetic technologies.
Today, the strongest anisotropy materials for permanent magnets depend heavily on rare-earth elements, which are expensive, environmentally damaging to mine and vulnerable to supply-chain disruptions and geopolitical instability. For thin film applications, certain alloys of iron and platinum have become the materials of choice for next generation magnetic recording media, which contain precious metal platinum. Finding high-performance alternatives based on earth-abundant elements has therefore been a long-standing scientific and technological challenge.
The “Joining” seems to connect people via radio waves. Let’s dig into the physics at play.
Join us on Patreon! https://www.patreon.com/MichaelLustgartenPhD
Discount Links/Affiliates:
Blood testing (where I get the majority of my labs): https://www.ultalabtests.com/partners/michaellustgarten.
At-Home Metabolomics: https://www.iollo.com?ref=michael-lustgarten.
Use Code: CONQUERAGING At Checkout.
Clearly Filtered Water Filter: https://get.aspr.app/SHoPY
Epigenetic, Telomere Testing: https://trudiagnostic.com/?irclickid=U-s3Ii2r7xyIU-LSYLyQdQ6…M0&irgwc=1
Use Code: CONQUERAGING
NAD+ Quantification: https://www.jinfiniti.com/intracellular-nad-test/
From the introduction:
“The inside story of the AI breakthrough that won a Nobel Prize.
-
The Thinking Game takes you on a journey into the heart of leading AI lab DeepMind, capturing a team striving to unravel the mysteries of intelligence and life itself.
Filmed over five years by the award winning team behind AlphaGo, the documentary examines how DeepMind co-founder Demis Hassabis’s extraordinary beginnings shaped his lifelong pursuit of artificial general intelligence. It chronicles the rigorous process of scientific discovery, documenting how the team moved from mastering complex strategy games to solving the 50-year-old “protein folding problem” with AlphaFold — a breakthrough that would win a Nobel Prize.”