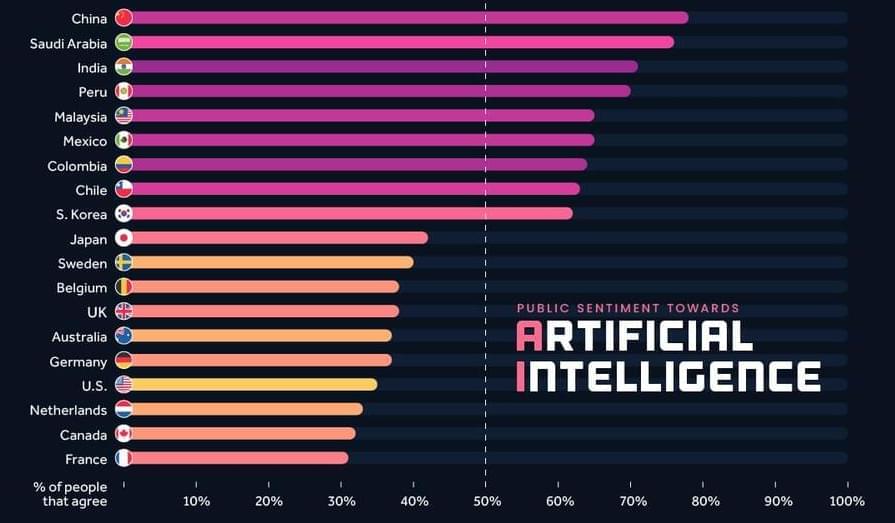
Interest in Earth-like planets orbiting within the habitable zone of their host stars has surged, driven by the quest to discover life beyond our solar system. But the habitability of such planets, known as exoplanets, is influenced by more than just their distance from the star.
A new study by Rice University’s David Alexander and Anthony Atkinson extends the definition of a habitable zone for planets to include their star’s magnetic field. This factor, well studied in our solar system, can have significant implications for life on other planets, according to the research published in The Astrophysical Journal on July 9.
The presence and strength of a planet’s magnetic field and its interaction with the host star’s magnetic field are pivotal factors in a planet’s ability to support life. An exoplanet needs a strong magnetic field to protect it from stellar activity, and it must orbit far enough from its star to avoid a direct and potentially catastrophic magnetic connection.