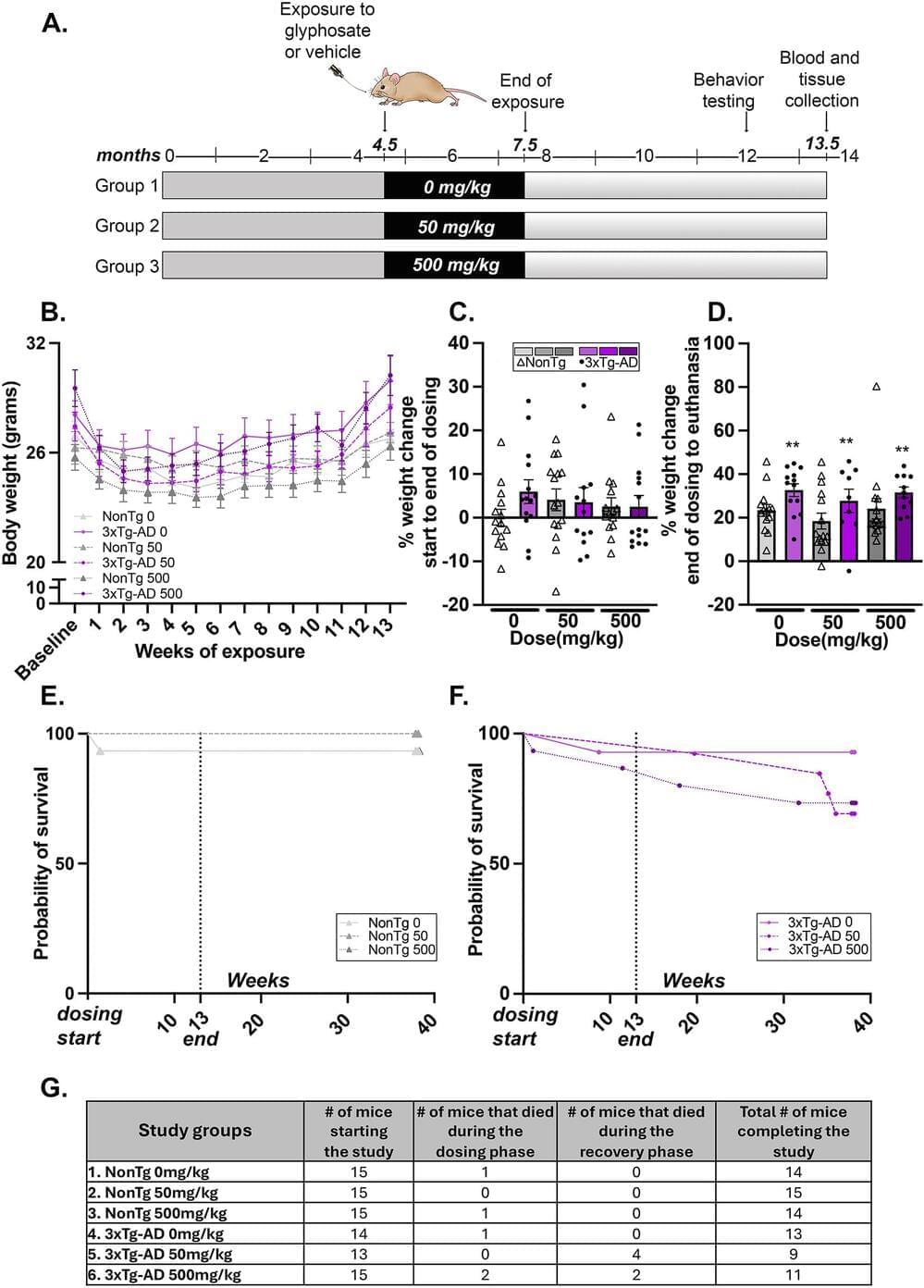
Glyphosate use in the United States (US) has increased each year since the introduction of glyphosate-tolerant crops in 1996, yet little is known about its effects on the brain. We recently found that C57BL/6J mice dosed with glyphosate for 14 days showed glyphosate and its major metabolite aminomethylphosphonic acid present in brain tissue, with corresponding increases in pro-inflammatory cytokine tumor necrosis factor-⍺ (TNF-⍺) in the brain and peripheral blood plasma. Since TNF-⍺ is elevated in neurodegenerative disorders such as Alzheimer’s Disease (AD), in this study, we asked whether glyphosate exposure serves as an accelerant of AD pathogenesis. Additionally, whether glyphosate and aminomethylphosphonic acid remain in the brain after a recovery period has yet to be examined.
We hypothesized that glyphosate exposure would induce neuroinflammation in control mice, while exacerbating neuroinflammation in AD mice, causing elevated Amyloid-β and tau pathology and worsening spatial cognition after recovery. We dosed 4.5-month-old 3xTg-AD and non-transgenic (NonTg) control mice with either 0, 50 or 500 mg/kg of glyphosate daily for 13 weeks followed by a 6-month recovery period.
We found that aminomethylphosphonic acid was detectable in the brains of 3xTg-AD and NonTg glyphosate-dosed mice despite the 6-month recovery. Glyphosate-dosed 3xTg-AD mice showed reduced survival, increased thigmotaxia in the Morris water maze, significant increases in the beta secretase enzyme (BACE-1) of amyloidogenic processing, amyloid-β (Aβ) 42 insoluble fractions, Aβ 42 plaque load and plaque size, and phosphorylated tau (pTau) at epitopes Threonine 181, Serine 396, and AT8 (Serine 202, Threonine 205). Notably, we found increased pro-and anti-inflammatory cytokines and chemokines persisting in both 3xTg-AD and NonTg brain tissue and in 3xTg-AD peripheral blood plasma.