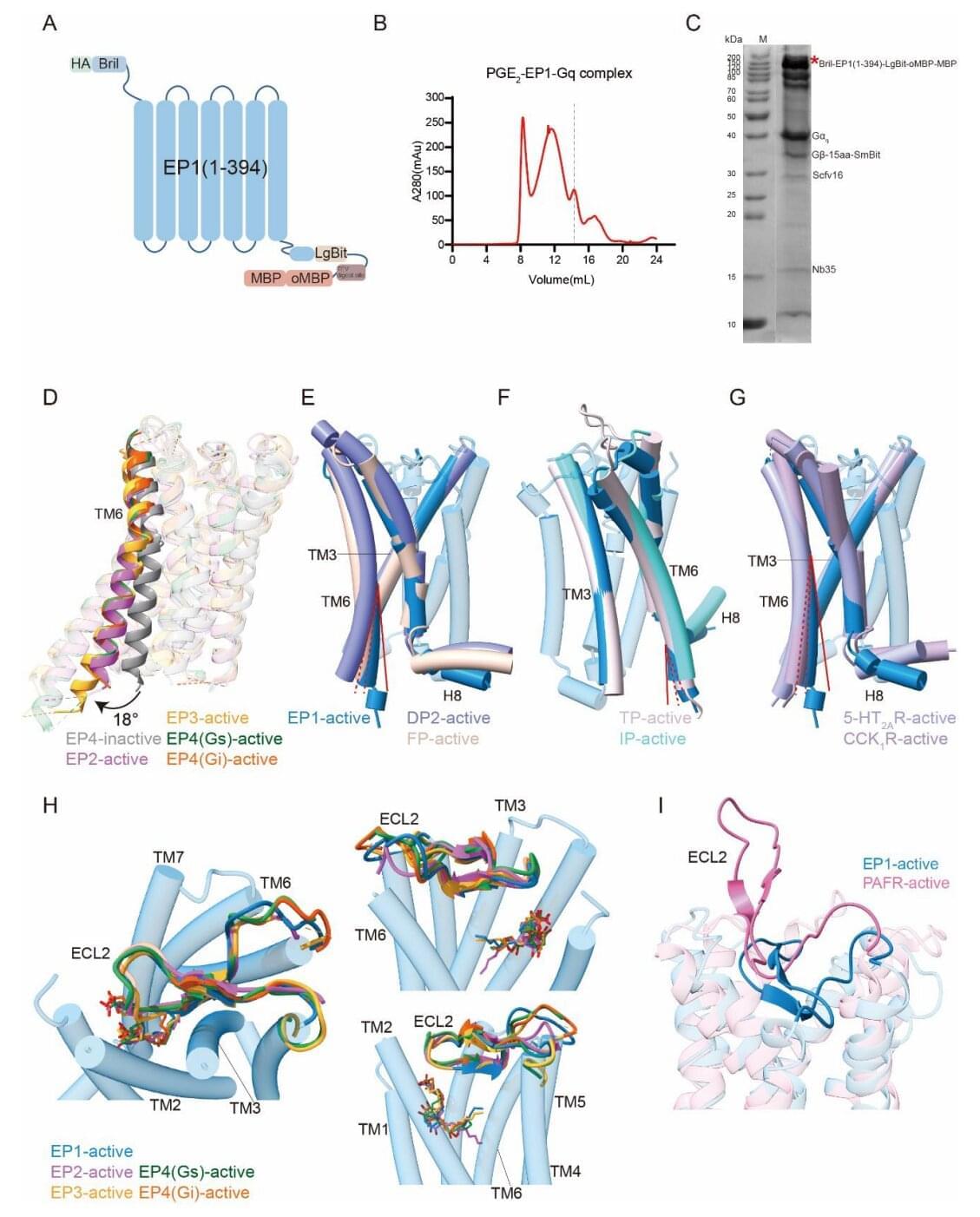
Prostaglandin E2 (PGE2), a bioactive lipid derived from arachidonic acid, mediates a broad range of physiological processes through four G protein-coupled receptor (GPCR) subtypes: EP1–EP4. While the high-resolution structures of EP2, EP3 and EP4 have been resolved, EP1 remained structurally uncharacterized due to its intrinsic instability, hindering detailed understanding of its Gq-mediated signaling.
In a study published in Proceedings of the National Academy of Sciences, a research team led by Eric H. Xu (Xu Huaqiang) and Xu Youwei from the Shanghai Institute of Materia Medica of the Chinese Academy of Sciences reported the cryo–electron microscopy (cryo-EM) structure of the human EP1 receptor in complexes with PGE2 and the heterotrimeric Gq protein, completed structural atlas of EP receptor family, and revealed EP1-specific mechanisms of ligand recognition and signal transduction.
To overcome the instability of EP1, the researchers employed a multi-pronged engineering strategy, including BRIL fusion, truncation of flexible loops, incorporation of a mini-Gq chimera, and NanoBiT-assisted complex stabilization. They resolved the structure of the EP1–PGE2–Gq complex at 2.55 Å resolution using single-particle cryo-EM, enabling detailed analysis of both ligand binding and G protein coupling interfaces.