A critical vulnerability in mcp-remote (CVE-2025–6514) allows remote code execution, affecting 437,000+ users.


The attack chains begin when one of these adversary-controlled accounts messages a victim through X, Telegram, or Discord, urging them to test out their software in exchange for a cryptocurrency payment.
Should the target agree to the test, they are redirected to a fictitious website from where they are promoted to enter a registration code provided by the employee to download either a Windows Electron application or an Apple disk image (DMG) file, depending on the operating system used.
On Windows systems, opening the malicious application displays a Cloudflare verification screen to the victim while it covertly profiles the machine and proceeds to download and execute an MSI installer. Although the exact nature of the payload is unclear, it’s believed that an information stealer is run at this stage.




Arabidopsis may seem like a simple plant, but at the University of Missouri, plant biochemist Jay Thelen is using it as a powerful model to explore ways to boost oil production—an important step toward creating more sustainable, plant-based energy sources.
To meet the increasing global demand for biofuels, scientists are already modifying plant genes to boost the amount of plant oil being produced. That’s because inside the plant, a complex network of metabolic pathways turns sunlight, carbon dioxide (or atmospheric carbon), water and nutrients into vital compounds including oil, the foundational ingredient of biofuel.
Genes give instructions to enzymes, and, in turn, those enzymes help control the plant’s metabolic pathways. But we are only beginning to understand how modifying these genes to produce more oil affects the plant’s other metabolic pathways, which are all interconnected.
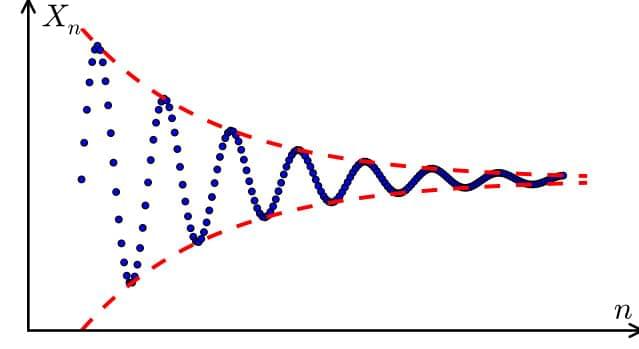
In mathematics, a Cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses. [ 1 ] More precisely, given any small positive distance, all excluding a finite number of elements of the sequence are less than that given distance from each other. Cauchy sequences are named after Augustin-Louis Cauchy; they may occasionally be known as fundamental sequences. [ 2 ].
Researchers also found that the treatment was safe and well-tolerated. Participants did not report any serious adverse reactions in the follow-up period of 6–12 months.
The most common reaction was a reduction in the number of the immune system’s neutrophils, a type of white blood cell.
“OTOF is just the beginning,” Dr Duan said, adding that researchers were working on other common genes behind deafness such as GJB2 and TMC1.