Lifeboat Foundation: Safeguarding Humanity
Toggle light / dark theme

Blog – Page 11

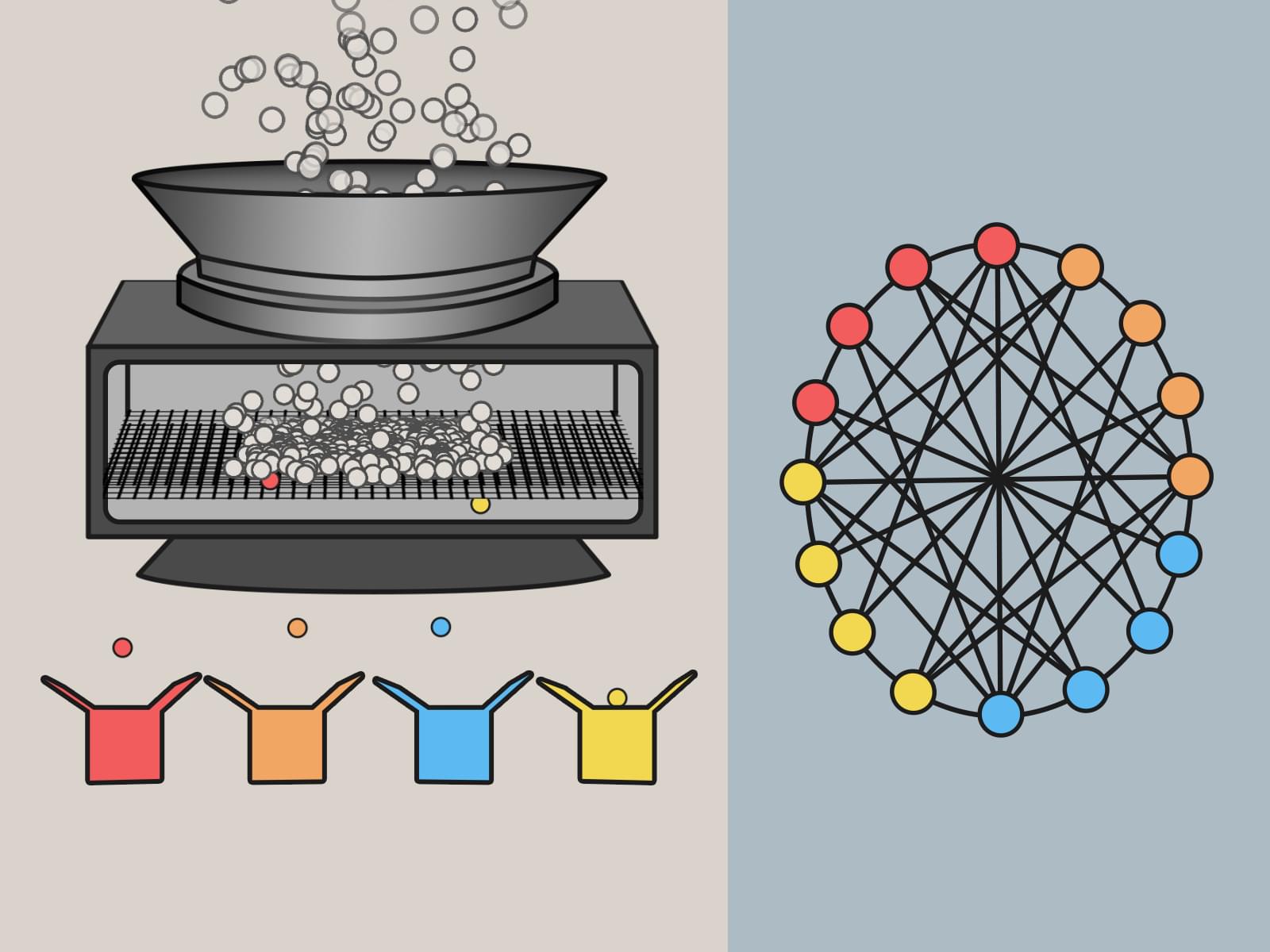
PRESS RELEASE — Quantum computers promise to speed calculations dramatically in some key areas such as computational chemistry and high-speed networking. But they’re so different from today’s computers that scientists need to figure out the best ways to feed them information to take full advantage. The data must be packed in new ways, customized for quantum treatment.

Researchers at the Department of Energy’s Pacific Northwest National Laboratory have done just that, developing an algorithm specially designed to prepare data for a quantum system. The code, published recently on GitHub after being presented at the IEEE International Symposium on Parallel and Distributed Processing, cuts a key aspect of quantum prep work by 85 percent.

While the team demonstrated the technique previously, the latest research addresses a critical bottleneck related to scaling and shows that the approach is effective even on problems 50 times larger than possible with existing tools.

Read more | >

Should you step away from the chicken wings?

For years, the conventional wisdom has been to swap out red meat for white meats like chicken and poultry to help reduce health risks like increased cholesterol, cancer, and inflammation —not to mention get a more budget-friendly protein source. But a new study links eating chicken and other poultry with a significantly increased risk of dying from gastrointestinal cancer and all other causes.

But before you put down the chicken—or roll your eyes and get back to your chicken Caesar—check out the details of the study, and what a dietitian says you should do if you’re concerned.

Read more | >

Understanding the origin of heavy elements on the periodic table is one of the most challenging open problems in all of physics. In the search for conditions suitable for these elements via “nucleosynthesis,” a Los Alamos National Laboratory-led team is going where no researchers have gone before: the gamma-ray burst jet and surrounding cocoon emerging from collapsed stars.

As proposed in an article in The Astrophysical Journal, photons produced deep in the jet could dissolve the outer layers of a star into neutrons, causing a series of physical processes that result in the formation of heavy elements.

“The creation of heavy elements such as uranium and plutonium necessitates extreme conditions,” said Matthew Mumpower, physicist at Los Alamos. “There are only a few viable yet rare scenarios in the cosmos where these elements can form, and all such locations need a copious amount of neutrons. We propose a new phenomenon where those neutrons don’t pre-exist but are produced dynamically in the star.”

Read more | >

The willingness of the 4f orbitals of lanthanide metals to participate in chemical reactions is as rare as their presence in Earth’s crust. A recent study, however, witnessed the 4f orbital in a cerium-based compound actively participate in bond formation, triggering a unique chemical reaction.

The researchers observed that a cerium-containing cyclic complex formed a 4f-covalent interaction, leading to a ring-opening isomerization from cyclopropene to allene. The findings are published in Nature Chemistry.

Lanthanides are heavy, rare-earth , occupying positions 57 through 71 in the —from lanthanum to lutetium—and are widely used in modern technologies ranging from electronics to clean energy. In nature, these elements are usually found together in their ore form and separating them using current methods is extremely challenging and energy-intensive. Understanding how these elements bond or interact with other atoms at an electronic level could help us to distinguish between lanthanides and design effective separation strategies.

Read more | >

In every scientific discovery in the movies, a scientist observes something unexpected, scratches the side of his or her forehead and says “hmmmmm.” In just such a moment in real life, scientists from Canada observed unexpected flashes of curved green light from a red light-emitting polymer above its surface. The flashes were reminiscent of the colored arcs that auroras take above Earth’s poles, providing a clue as to their provenance.

Their resulting investigation of the new phenomenon could find applications towards understanding the failures of polymer materials and more. Their work has been published in Physical Review Letters.

Jun Gao, a professor and chair of Engineering Physics at the Engineering Physics and Astronomy Department at Queen’s University in Ontario, Canada, and graduate student Dongze Wang were investigating the performance of semiconductors called polymer light-emitting electrochemical cells, or PLECs.

Read more | >

As artificial intelligence (AI) continues to advance, researchers at POSTECH (Pohang University of Science and Technology) have identified a breakthrough that could make AI technologies faster and more efficient.

Professor Seyoung Kim and Dr. Hyunjeong Kwak from the Departments of Materials Science & Engineering and Semiconductor Engineering at POSTECH, in collaboration with Dr. Oki Gunawan from the IBM T.J. Watson Research Center, have become the first to uncover the hidden operating mechanisms of Electrochemical Random-Access Memory (ECRAM), a promising next-generation technology for AI. Their study is published in the journal Nature Communications.

As AI technologies advance, data processing demands have exponentially increased. Current computing systems, however, separate data storage (memory) from data processing (processors), resulting in significant time and due to data transfers between these units. To address this issue, researchers developed the concept of in-memory computing.

Read more | >

Imagine if our computers could think more like us—learning from experience, adapting on the go, and doing all this while using just a fraction of the energy. That’s not science fiction anymore. Welcome to the world of Neuromorphic Computing 🧠—a field that’s redefining how machines process information by taking inspiration from the most powerful processor we know: the human brain.

Read more | >

In this second episode of the AI Bros podcast Bruce and John go completely unscripted and just letting the conversation flow where it goes.

They talk about everything from Sam Altman’s controversial TED interview to John’s Animated Action Figure that came to life and broke out of its packaging. It’s interesting, fun and informative.

Subscribe, Like, Follow, and Share the AI Bros to your favorite social media platforms. The AI Bros Podcast is where artificial intelligence meets real talk.

Both Bruce and John share their hot takes, perspective and journey with AI as they learn it and use it themselves in their own day to day workflow.

The AI Bros podcast is a weekly series, and a part of the Neural News Network, and the (A)bsolutely (I)ncredible podcast channel. John Lawson III is the CEO of ColderICE Media and is highly recognized in e-commerce, and AI.

John is an Amazon #1 best-selling author, IBM Futurist, and an eBay Influencer.

He’s celebrated as one of the Top 100 Small Business Influencers in America, and crowned “Savviest in Social Medial” by StartUp Nation. You can connect with John directly on his website at www.johnlawson. comJohn is an internationally-recognized keynote speaker, a “Commerce Evangelist” and an absolute wealth of knowledge on all things e-retail, and online marketing strategy.

John is a pioneer in the online retail vertical space, and founder of The E-commerce Group, a global community of e-commerce vendors, and online marketers.

Continue reading “The AI Bros Podcast, With Bruce Burke and John Lawson III” | >