A natural compound from broccoli sprouts that’s now backed by science for brain health, aging, cancer, metabolism, and more.


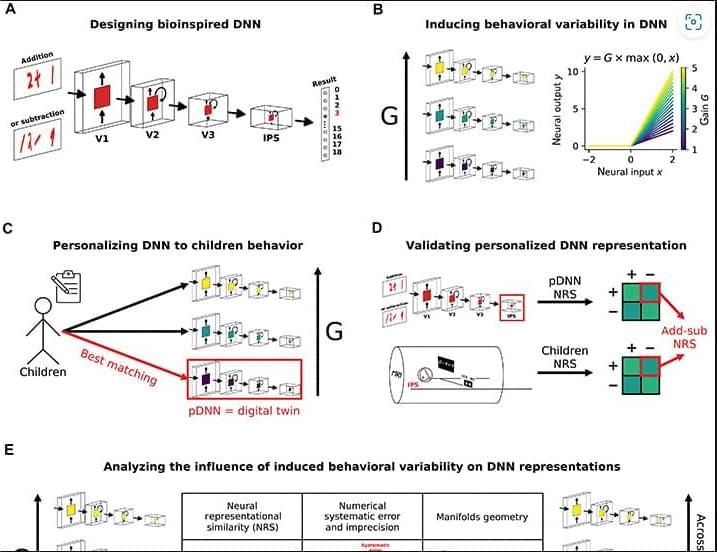
N6-methyladenosine (m6A) is the most common and abundant endogenous mRNA methylation in eukaryotic cells (Huang et al., 2020; Wang et al., 2014). The regulation of this modification is achieved through the coordinated action of three distinct protein groups. The “writers” (methyltransferase complex), which include METTL3, METTL14, and WTAP, are responsible for adding the m6A modification. In contrast, the “erasers” (demethylases), which consist of FTO and ALKBH5, remove this chemical mark. Lastly, the “readers,” a group of proteins including YTHDF1/2/3 and YTHDC1/2, recognize and bind to m6A-modified RNA, thereby modulating diverse RNA metabolic processes. The m6A reader proteins YTHDFs exhibit distinct canonical functional roles: YTHDF1 primarily boosts the efficiency of mRNA translation, YTHDF2 enhances mRNA degradation, and YTHDF3 exerts dual functions by supporting both translation and degradation of mRNA, with its role varying depending on the specific biological context (Roundtree et al., 2017; Shi et al., 2017; Wang et al., 2014; Wang et al., 2015; Zaccara et al., 2019). Recent studies have revealed that YTHDF proteins can influence the efficacy of RT through mechanisms, such as modulating DNA repair and shaping the tumor immune microenvironment (TIME) (Du et al., 2023; Shao et al., 2023; Shi et al., 2023; Wang et al., 2023a; Wang et al., 2023c; Wen et al., 2024a; Yin et al., 2023). Elucidating the functions and mechanisms of YTHDF proteins within the context of radiation biology holds significant potential for advancing therapeutic strategies in cancer RT.
This review provides an overview of recent progress in elucidating the mechanisms by which YTHDF proteins in tumor and immune cells modulate the therapeutic efficacy of RT. By synthesizing current knowledge on the functions of YTHDF proteins in the context of IR, we emphasize their indispensable role in shaping RT outcomes.
In this study, Jung et al. investigate the effect of excessive NLRP3-mediated neuroinflammation on synaptic functions and behaviors using Nlrp3D301N-conditional knockin mice. Strikingly, excessive NLRP3-mediated neuroinflammation causes NMDAR hyperactivation, leading to abnormal behaviors. Treatment with IL-1β receptor antagonist (IL-1RA) or NMDAR antagonist reverses the pathological phenotypes.
Rice and Baylor researchers have used Rice’s “drug factory” implants to eradicate advanced-stage mesothelioma tumors in mice.

Heat causes errors in the qubits that are the building blocks of a quantum computer, so quantum systems are typically kept inside refrigerators that keep the temperature just above absolute zero (−459 degrees Fahrenheit).
But quantum computers need to communicate with electronics outside the refrigerator, in a room-temperature environment. The metal cables that connect these electronics bring heat into the refrigerator, which has to work even harder and draw extra power to keep the system cold. Plus, more qubits require more cables, so the size of a quantum system is limited by how much heat the fridge can remove.
To overcome this challenge, an interdisciplinary team of MIT researchers has developed a wireless communication system that enables a quantum computer to send and receive data to and from electronics outside the refrigerator using high-speed terahertz waves.
(From 2023)
A new wireless terahertz communication system enables a super-cold quantum computer to send and receive data without generating too much error-causing heat.

The researchers identified a stress response that emerges from damaged mitochondria. By interrupting this stress response with a compound known as ISRIB, their results showed a marked improvement in blood sugar handling in mice.
A β-cell in the pancreas is responsible for releasing insulin, the hormone that regulates blood sugar.
These cells need high energy output from mitochondria to carry out their job. Weak energy conversion can disrupt insulin release, fueling the symptoms associated with type 2 diabetes.

On 23 June 2025, the world will get a look at the first images from one of the most powerful telescopes ever built: the Vera C. Rubin Observatory.
Perched high in the Chilean Andes, the observatory will take hundreds of images of the southern hemisphere sky, every night for 10 years. In doing so, it will create the most complete time-lapse record of our universe ever assembled. This scientific effort is known as the Legacy Survey of Space and Time (LSST).
Rather than focusing on small patches of sky, the Rubin Observatory will scan the entire visible southern sky every few nights. Scientists will use this rolling deep-sky snapshot to track supernovae (exploding stars), asteroids, black holes, and galaxies as they evolve and change in real time. This is astronomy not as a static snapshot, but as a cosmic story unfolding night by night.